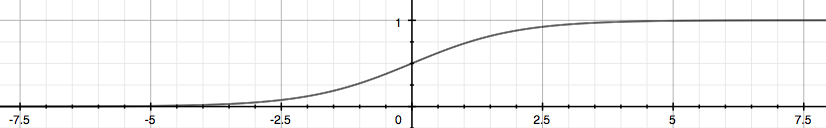2 changed files with 19 additions and 1 deletions
Unified View
Diff Options
BIN
notes/image/2413fbec8ff9fa1f19aaf78265b8a33b_Logistic_function.png
View File
+ 19
- 1
notes/week3.md
View File
| @@ -14,7 +14,7 @@ | |||||
|  |  | ||||
| 肿瘤诊断问题是一个二元分类问题,则定义 $ y \in\lbrace 0, 1\rbrace$,其中 0 表示**负向类(negative class)**,代表恶性肿瘤,1 为**正向类(positive class)**,代表良性肿瘤。如图,定义最右边的样本为**偏差项**。 | |||||
| 肿瘤诊断问题是一个二元分类问题,则定义 $ y \in\lbrace 0, 1\rbrace$,其中 0 表示**负向类(negative class)**,代表恶性肿瘤("-"),1 为**正向类(positive class)**,代表良性肿瘤("+")。如图,定义最右边的样本为**偏差项**。 | |||||
| 在未加入偏差项时,线性回归算法给出了品红色的拟合直线,若规定 | 在未加入偏差项时,线性回归算法给出了品红色的拟合直线,若规定 | ||||
| @@ -36,7 +36,25 @@ $h_\theta(x) \lt 0.5$ ,预测为 $y = 0$,即负向类。 | |||||
| ## 6.2 假设函数表示(Hypothesis Representation) | ## 6.2 假设函数表示(Hypothesis Representation) | ||||
| 为了使 $h \in \left(0, 1\right)$,引入逻辑回归模型,定义假设函数 | |||||
| $$ | |||||
| h_\theta \left( x \right)=g\left(\theta^{T}X \right) | |||||
| $$ | |||||
| 对比线性回归函数 $h_\theta \left( x \right)=\theta^{T}X$,$g$ 表示逻辑函数(logistic function),复合起来,则为线性回归函数。 | |||||
| 一个常用的逻辑函数是 S 形函数,叫做 **sigmoid 函数**(如下图),其公式为 $g\left( z \right)=\frac{1}{1+{{e}^{-z}}}$。 | |||||
|  | |||||
| 应用 sigmoid 函数,则逻辑回归模型:$$h_{\theta}(x)=g(\theta^Tx) =\frac{1}{1+e^{-\theta^Tx}}$$ | |||||
| $h_\theta \left( x \right)$ 的作用是,根据输入 $x$,参数 $\theta$ 计算得出”输出 $y=1$“的可能性(estimated probability),概率学中表示为: | |||||
| $\begin{align*}& h_\theta(x) = P(y=1 | x ; \theta) = 1 - P(y=0 | x ; \theta) \newline & P(y = 0 | x;\theta) + P(y = 1 | x ; \theta) = 1\end{align*}$ | |||||
| 以肿瘤诊断为例,$h_\theta \left( x \right)=0.7$ 表示有 $70\%$ 的概率为恶性肿瘤。 | |||||
| ## 6.3 Decision Boundary | ## 6.3 Decision Boundary | ||||