machinelearning_notebook/6_pytorch/1_NN/optimizer/6_6-adam.ipynb

{
 "cells": [
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "# Adam\n",
    "Adam 是一个结合了动量法和 RMSProp 的优化算法，其结合了两者的优点。\n",
    "\n",
    "## Adam 算法\n",
    "Adam 算法会使用一个动量变量 v 和一个 RMSProp 中的梯度元素平方的移动指数加权平均 s，首先将他们全部初始化为 0，然后在每次迭代中，计算他们的移动加权平均进行更新\n",
    "\n",
    "$$\n",
    "v = \\beta_1 v + (1 - \\beta_1) g \\\\\n",
    "s = \\beta_2 s + (1 - \\beta_2) g^2\n",
    "$$\n",
    "\n",
    "在 adam 算法里，为了减轻 v 和 s 被初始化为 0 的初期对计算指数加权移动平均的影响，每次 v 和 s 都做下面的修正\n",
    "\n",
    "$$\n",
    "\\hat{v} = \\frac{v}{1 - \\beta_1^t} \\\\\n",
    "\\hat{s} = \\frac{s}{1 - \\beta_2^t}\n",
    "$$\n",
    "\n",
    "这里 t 是迭代次数，可以看到，当 $0 \\leq \\beta_1, \\beta_2 \\leq 1$ 的时候，迭代到后期 t 比较大，那么 $\\beta_1^t$ 和 $\\beta_2^t$ 就几乎为 0，就不会对 v 和 s 有任何影响了，算法作者建议$\\beta_1 = 0.9$, $\\beta_2 = 0.999$。\n",
    "\n",
    "最后使用修正之后的 $\\hat{v}$ 和 $\\hat{s}$ 进行学习率的重新计算\n",
    "\n",
    "$$\n",
    "g' = \\frac{\\eta \\hat{v}}{\\sqrt{\\hat{s} + \\epsilon}}\n",
    "$$\n",
    "\n",
    "这里 $\\eta$ 是学习率，$epsilon$ 仍然是为了数值稳定性而添加的常数，最后参数更新有\n",
    "\n",
    "$$\n",
    "\\theta_i = \\theta_{i-1} - g'\n",
    "$$"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "下面我们来实现以下 adam 算法"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 1,
   "metadata": {},
   "outputs": [],
   "source": [
    "def adam(parameters, vs, sqrs, lr, t, beta1=0.9, beta2=0.999):\n",
    "    eps = 1e-8\n",
    "    for param, v, sqr in zip(parameters, vs, sqrs):\n",
    "        v[:] = beta1 * v + (1 - beta1) * param.grad.data\n",
    "        sqr[:] = beta2 * sqr + (1 - beta2) * param.grad.data ** 2\n",
    "        v_hat = v / (1 - beta1 ** t)\n",
    "        s_hat = sqr / (1 - beta2 ** t)\n",
    "        param.data = param.data - lr * v_hat / torch.sqrt(s_hat + eps)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 2,
   "metadata": {},
   "outputs": [],
   "source": [
    "import numpy as np\n",
    "import torch\n",
    "from torchvision.datasets import MNIST # 导入 pytorch 内置的 mnist 数据\n",
    "from torch.utils.data import DataLoader\n",
    "from torch import nn\n",
    "from torch.autograd import Variable\n",
    "import time\n",
    "import matplotlib.pyplot as plt\n",
    "%matplotlib inline\n",
    "\n",
    "def data_tf(x):\n",
    "    x = np.array(x, dtype='float32') / 255\n",
    "    x = (x - 0.5) / 0.5 # 标准化，这个技巧之后会讲到\n",
    "    x = x.reshape((-1,)) # 拉平\n",
    "    x = torch.from_numpy(x)\n",
    "    return x\n",
    "\n",
    "train_set = MNIST('../../../data/mnist', train=True, transform=data_tf, download=True) # 载入数据集，申明定义的数据变换\n",
    "test_set  = MNIST('../../../data/mnist', train=False, transform=data_tf, download=True)\n",
    "\n",
    "# 定义 loss 函数\n",
    "criterion = nn.CrossEntropyLoss()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 3,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "epoch: 0, Train Loss: 0.372057\n",
      "epoch: 1, Train Loss: 0.186132\n",
      "epoch: 2, Train Loss: 0.132870\n",
      "epoch: 3, Train Loss: 0.107864\n",
      "epoch: 4, Train Loss: 0.091208\n",
      "使用时间: 85.96051 s\n"
     ]
    }
   ],
   "source": [
    "train_data = DataLoader(train_set, batch_size=64, shuffle=True)\n",
    "# 使用 Sequential 定义 3 层神经网络\n",
    "net = nn.Sequential(\n",
    "    nn.Linear(784, 200),\n",
    "    nn.ReLU(),\n",
    "    nn.Linear(200, 10),\n",
    ")\n",
    "\n",
    "# 初始化梯度平方项和动量项\n",
    "sqrs = []\n",
    "vs = []\n",
    "for param in net.parameters():\n",
    "    sqrs.append(torch.zeros_like(param.data))\n",
    "    vs.append(torch.zeros_like(param.data))\n",
    "t = 1\n",
    "# 开始训练\n",
    "losses = []\n",
    "idx = 0\n",
    "\n",
    "start = time.time() # 记时开始\n",
    "for e in range(5):\n",
    "    train_loss = 0\n",
    "    for im, label in train_data:\n",
    "        im = Variable(im)\n",
    "        label = Variable(label)\n",
    "        # 前向传播\n",
    "        out = net(im)\n",
    "        loss = criterion(out, label)\n",
    "        # 反向传播\n",
    "        net.zero_grad()\n",
    "        loss.backward()\n",
    "        adam(net.parameters(), vs, sqrs, 1e-3, t) # 学习率设为 0.001\n",
    "        t += 1\n",
    "        # 记录误差\n",
    "        train_loss += loss.data[0]\n",
    "        if idx % 30 == 0:\n",
    "            losses.append(loss.data[0])\n",
    "        idx += 1\n",
    "    print('epoch: {}, Train Loss: {:.6f}'\n",
    "          .format(e, train_loss / len(train_data)))\n",
    "end = time.time() # 计时结束\n",
    "print('使用时间: {:.5f} s'.format(end - start))"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 4,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "<matplotlib.legend.Legend at 0x10d707908>"
      ]
     },
     "execution_count": 4,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAD8CAYAAAB+UHOxAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztvXd4HNd57/89uzPbCzoIEOyUKJKiigU1S7aluEmWZEmJ\nHdlJHOdGsZzE9s2Nn8SP067l3BvbUWIn146TXxRFcYl7jeVILrJVrGqS6mIRKVaQIDq2l5nZ8/tj\n5pyd3Z1dLIFtAN7P8/AhudhyZhd73vN+38Y45yAIgiBWH652L4AgCIJoD2QACIIgVilkAAiCIFYp\nZAAIgiBWKWQACIIgVilkAAiCIFYpZAAIgiBWKWQACIIgVilkAAiCIFYpSrsXUIu+vj6+cePGdi+D\nIAhi2bB3795pznl/PfftaAOwceNG7Nmzp93LIAiCWDYwxo7Xe9+OlIAYYzcxxu6OxWLtXgpBEMSK\npSMNAOf8Ps75HdFotN1LIQiCWLF0pAEgCIIgmk9HxwAIgiBqoWkaxsbGkM1m272UluPz+TAyMgJV\nVRf9HGQACIJYtoyNjSEcDmPjxo1gjLV7OS2Dc46ZmRmMjY1h06ZNi34ekoAIgli2ZLNZ9Pb2rqrN\nHwAYY+jt7V2y50MGgCCIZc1q2/wFjbjuFWkAvvD4UfzwhdPtXgZBEERHsyINwFd/eQI/fH683csg\nCIIAAHzhC1/ABz/4wXYvo4IVaQAiPhXxrNbuZRAEQXQ0K9MA+FUksnq7l0EQxCrhlltuwSWXXIKd\nO3fi7rvvBgD8x3/8B84991xcdtllePzxx+V977vvPlx++eW4+OKL8aY3vQkTExMAgDvvvBPvfe97\n8brXvQ4bNmzAd7/7XXzkIx/Brl27cN1110HTGn+oXZFpoGGfglenku1eBkEQLeTj972MfafjDX3O\nHcMRfOymnQve795770VPTw8ymQwuvfRS3HDDDfjYxz6GvXv3IhqN4tprr8XFF18MALj66qvx1FNP\ngTGGe+65B3fddRc+/elPAwBeffVVPPTQQ9i3bx+uvPJKfOc738Fdd92FW2+9Ff/93/+NW265paHX\ntyINQMSnIp4hCYggiNbw2c9+Ft/73vcAACdPnsSXv/xlXHPNNejvN5ty3nbbbXjllVcAmLULt912\nG8bHx5HP50vy+K+//nqoqopdu3bBMAxcd911AIBdu3bh2LFjDV/3yjQAfgXxrA7O+apNESOI1UY9\nJ/Vm8PDDD+PBBx/Ek08+iUAggGuuuQbnnXce9u3b53j/D33oQ/jwhz+Mt7/97Xj44Ydx5513yp95\nvV4AgMvlgqqqcv9yuVzQ9cbL2h0ZA1hqN9CwT4VR4MhoRoNXRhAEUUosFkN3dzcCgQAOHDiAp556\nCplMBo888ghmZmagaRq+9a1vldx/7dq1AIAvfvGL7Vo2gA41AEvtBhrxmb0x4hkKBBME0Vyuu+46\n6LqO7du346Mf/SiuuOIKDA0N4c4778SVV16Jq666Ctu3b5f3v/POO/HOd74Tl1xyCfr6+tq4coBx\nztu6gFqMjo7yxQyE+eELp/HBrz6Ln/zx63HuYLgJKyMIohPYv39/yea62nC6fsbYXs75aD2P70gP\nYKmELQ8gQbUABEEQVVmRBiDiM2PbJAERBEFUZ2UaAL8VAyAPgCBWPJ0sYzeTRlz3ijQAYeEBUDUw\nQaxofD4fZmZmVp0REPMAfD7fkp5nZdYByCwg8gAIYiUzMjKCsbExTE1NtXspLUdMBFsKK9IA+FQ3\nPIqLJCCCWOGoqrqkiVirnRUpAQFmIJgawhEEQVRnBRsA6gdEEARRixVrAMJ+lYLABEEQNVixBsCU\ngMgDIAiCqMYKNgAkAREEQdRi5RoAqyU0QRAE4cyKNQBhn0oSEEEQRA1WrAGI+BRktQJyOs0EIAiC\ncGLlGgC/6AhKMhBBEIQTK9YAiH5AZAAIgiCcaVkrCMZYEMA/A8gDeJhz/pVmvh71AyIIgqjNkjwA\nxti9jLFJxthLZbdfxxg7yBg7zBj7qHXzrwL4Nuf8fQDevpTXrQdqCU0QBFGbpUpAXwBwnf0Gxpgb\nwOcBXA9gB4B3M8Z2ABgBcNK6W9MjsyQBEQRB1GZJBoBz/iiA2bKbLwNwmHN+hHOeB/B1ADcDGINp\nBJb8uvVAEhBBEERtmrERr0XxpA+YG/9aAN8F8GuMsX8BcF+1BzPG7mCM7WGM7VlKj2+SgAiCIGrT\nsiAw5zwF4H/Ucb+7AdwNAKOjo4se8xP0uOFiJAERBEFUoxkewCkA62z/H7FuaymMMYSpHxBBEERV\nmmEAdgM4hzG2iTHmAfAuAD9owussSHdAxXQq346XJgiC6HiWmgb6NQBPAtjGGBtjjN3OOdcBfBDA\njwHsB/BNzvnLZ/m8NzHG7o7FYktZHtZEfZiIZZf0HARBECuVJcUAOOfvrnL7/QDuX8Lz3gfgvtHR\n0fct9jkAYE3Ehz3H55byFARBECuWFdsKAgAGoz5MxnMoFBYdSyYIglixrGgDMBTxIW8UMJumOABB\nEEQ5HWkAGhkDAIAzFAcgCIKooCMNAOf8Ps75HdFodEnPMxgxDcBEnAwAQRBEOR1pABrFUNQPABgn\nD4AgCKKCFW0A+kIeuBh5AARBEE50pAFoVAxAcbvQH/ZSDIAgCMKBjjQAjYoBAMCaqB9nyAMgCIKo\noCMNQCNZEyEPgCAIwolVYAB85AEQBEE4sPINQNSPRFZHKkdtoQmCIOx0pAFoVBAYANZEvQBQ1QvI\nagbe96U9ODyZXPJrEQRBLCc60gA0NAgcMWsBqnUFPXgmgZ/um8BDByaX/FoEQRDLiY40AI1EtoOo\n4gGMxzIAgOOzqZatiSAIohNY+QbAagdRrRr49Lx5+/GZdMvWRBAE0QmseAPg97gxFPXh5wcmHdtC\nCw/gxCwZAIIgVhcr3gAAwB+/+VzsPT6H7zwzVvGz05ZncGouA90otHppBEEQbWNVGIB3vGYEl2zo\nxicfOID5stkA4/OmB6AXuJSD6uHBfRN4191PtmTYTFYz8Kffel56KwRBEI2gIw1AI9NAAcDlYvi/\nt5yP+XQe9z52tORn47EsRrrNTKGzCQR/c89JPHVkFrGM1pA1fvXpE3hlIuH4s4NnEvjW3jE8cXim\nIa9FEAQBdKgBaGQaqGD7UASjG3rwM1u6p24UMBHP4orNvQDqDwTrRgFPvmpuxo2YNqYbBfzF91/E\nV5467vjzOes14tnGGBuCIAigQw1As3jDtn68fDqOSSsldDKRQ4EDF63rgkdx1R0IfuFUDAmrsrhc\nUloMc2kNnANTyZzjz+fT5sYfz1A1M0EQjWNVGYBrtvUDAB5+ZQpAMQNobbcf67r9OD5TnwT02KFp\n+e/Z1NJP5bMp04hMxp0NgPh5gjwAgiAayKoyADuGIhgIe/HIQdMAiKDvcNSPDb3BuiWgxw5Poy/k\nAQDMpZbuAcxYJ//qHgBJQARBNJ5VZQAYY3jDuf34xaEp6EZBegBDXT6s7wngxGwanNfO6knldDx7\nYg5v2zUEoKjPL4Vpmwfg9PpzJAERBNEEVpUBAIBrtg0gntXx7Ml5nJ7PIuRVEPGp2NAbQDpvYGaB\nE/1DByehGRxv2bEGHsXVkCDwrHXyz2gGUnmj8ufkARAE0QQ60gA0Og3UztXn9MHjduFbe07i9HwG\nQ1avoA29AQCoGgfgnOMrTx/Hh7/xPDb2BjC6sRvdARXzDYgB2I1OMUCdhWHVGAgJKJElD4AgiMbR\nkQagGWmggqhfxW9esR7f3juG507OY6jLrAHYMRSFx+3Cpx44gKxWeQr/+YFJ/MX3XsKVW3rx/Q9c\nBZ/qRnfA0xAPYDpZfI6pRA6xjIY33PWwrFyes4wMeQAEQTSSjjQAzeYD126FT3VjMpHDsOUBrIn6\n8OlfvxC7j83hT771fEWF74unYmAMuPu3L0FXwAwA9wQ9DQkCz6ZyUN0MgJma+upUEhnNwCGrMEzW\nATSo6IwgCAJYpQagL+TF7VdvAgAMRf3y9psuHMafvnUbfvjCOJ54tbTq9sRsGkMRH7yKW97WHfBU\nDQL/6KUz+MLjRx1/Vs5MMo8t/SEApgdwZMqUoUSfojmbBLRQkJogCKJeVqUBAIDfe91mvHZLL64+\np7fk9vdcuQEA8MKp+ZLbT86msa4nUHJbd1CVGTrlfGP3CfzDg4fq2rBnUqYBUN0Mk4kcjk6b08nG\n5zPI5A1ktQKifhV6gSPjIE8RBEEshlVrAKJ+FV993xW4ZENPye0Rn4qRbj/2nY6X3H5iNo315QYg\n4MF8Ou/YEC6R1RHLaPIUX4uZZA79YS/6Ql5MJrLSAxiPZeXpXwSpa6WCcs6RpNnHBEHUyao1ALXY\nMRTBvvGiAchqBibiOUcDUODOwVlxW7khKSevFxDP6ugJejAQ9mIqkcPRadMATMSzmLECxOK1awWC\n73/xDF7zf36KF8bmq96HIAhCQAbAgR3DERydTiGdN0/TY3NmhfD63koJCCi2arAjUjb3j9c2AOKx\nvSEP+sNeTMSzODqdQsSnoMCBA2fMxwsPoFY7iBOzaeT1Av74G885ZjI1Es457n3sKKYSztXLBPDn\n33sR//XcqXYvgyCqQgbAgR1DEXButmEGitPCKmIAVjaQUxxAGICFPICZlLmB9gY96A/7cHgyiZxe\nkB1KhSeyoScIoLYEJLyDV6dSuOtHB2u+7lI5NZ/BX/9wH+57/nRTX2c588PnT+PRV6YXviNBtAky\nAA7sGI4AKG6+J6weQU4SEFDZD8goFLX4fQt4AELi6Q15MRD2QoQTrj6nz3y8ZUCE91FLAopnNPQE\nPXj3ZevwH08cbWo8QNQmNKIVxkoloxnIaBSTITqXjjQAzawEroe1XX5EfIrcfE/MZhDwuNEb9JTc\nrycoPIDSTTBpnf57gx6cmE3XlG1KPQCvvP21W0wDICSkYgyg+oaSyOqI+BRcurHHbC/dRHlGFMA5\nyV8EoBkFaAZH2qG1B0F0Ch1pAJpZCVwPjDFstwWCRQYQY6zkft1VDIA4pV++2cwwOnDGedIXYPMA\ngqYHAAAhr4It/UEEPW7EszpCXkUam1rFYPGshrBPRV/IfB5hAL705DHc/E+PyftpRgE5fWkbk/B6\nyANwRmz8ZACITqYjDUAnsGM4ggPjCRgF7lgDAABBjxuqm1XMBJAGYJOl49eIA8yk8lBcDBG/Ij2A\nzf1BMMZkm4ruoAqf6oZHcdWUgBJZveR5pq0mc88cn8MLp2IyXfUT9+/He+755YLvwb2PHcUTh501\nbHHyn2tAL6SVSMba+DNkAIgOhgxAFXYMRZDRDLx0KuZYAwCYnoKoBbAjAsBbB0LoCXrwjd0nces/\nP46PfueFipqBmWQOPUEPGGMYiJhtKTb1mQFf0ahOxBoiPrV2EDijIeLgAZyJZ8F5cV1HplI4YhWb\n1eJzPz+E/3y69phK8gCcERlk4m+C6ETIAFThmm0D6A168IdfeQYZzXA0AIC5OZfr4GKjjfhUvGZ9\nN/aNxxFLa/j67pP4x58dKrnvbCqPXmvD7gt5EPS4cf6wKX0NW20quqQBUGrGE0wJyJSLXKzoAYhJ\nY2KA/XxGQyyjLTz7IG9UHZMprpliAM6kyQMglgFKuxfQqfSHvfjcb1yM9/y7KZVUNQBBtTIGYG20\nYZ+Cf7jtQqTzBgbCXnzk2y/gsz87hHMHQ7jxgmEAZidQMV3Mq7jx0w+/QZ7g11geQE/ArDcI+9U6\ngsAq3C6GnqBXegATVotpYQDiGQ2awZHVCvB73I7PpRkF5PUCTs5mHH8urnk+bRqS8vjIakfGAKh1\nB9HBkAdQg9du6cNf3rAdqpth25qw433MhnClp3JxSg/7FIR9KgYjPjDG8De37sKOoQg+97PD8r4z\nqZwM8ALAcJcfHsVl/ds0AHYPoFoQWDMKSOcNhH2msegPezGdzCGZ0+WQGekBWJt3rEZAOZ0rPsbp\nfuLknzcKjkNsVjtFCYjeG6JzIQOwAP/jqk148c63YrjL7/jzboeW0EICEpuxwKO48I5LRnBwIoEj\nU0mcns/g1FwGm/tCjs8tOpXaYwDVJCApO/lNp64v5MFUIidP/4C5mRcKXG7otQxAyqZdn3SQgezB\n30a0xK6XD3zlGXz6J80tcmsEQvrJ6wU52IcgOg0yAHXgU51lEgDosVpC27/k8awGn+qSJ3k7152/\nBgDwo5fP4Nt7x1DgwK0Xr3V8bmF0eqyWExG/UlUCEoYhUuIB5DERKzUAybwui81qegA2AyBaYdiZ\nTedltlErA8FPvDqNl061pz7kbLCf/CkQTHQqZACWSL9VvWsPhiayesXpXzDc5ceF67pw/4vj+Oae\nk3jtlt6KHkOCLf1B/O8bd+AGK15gZgE5b9oiOyjsMz2A/pAXU8kczpR5ADGbXFXTA8gVN7DyQDDn\nHHOpPDZb2UqtCgRn8gbm0tqykFXs2j8FgolOhQzAEhHFW/aqW1GRW43rdq7BS6fiGJvL4LZL11W9\nH2MMv3v1JhkjCPsU5HTnIi7pAfiLHkBeL+DwZNJ6rko9v1ZRWSpnl4BKA8GJnA69wLFlwJSuWuUB\nnI6Z61gOMxEytlP/cjBYxOqEDMASETLIZKJ40hYVudW43pKBIj4Fb925pu7XEpu703D4eJkEJDKJ\nXj4dR8iroDfoqTAAtWMA5qaluBhOlklAQvMXU8xaVQw2Pm++x8thQy2VgDp/vcTiuPexo3ju5PJt\nv04GYIkMhM1MHbsHEM/qcrN2YmNfEG/aPojfe93mmvGFcsTm7nRyr5CAwsIAxDAQ8SLiVxHP1m8A\nhG69dSBUIQEJyWdjbwAuVuoBcM6x9/hcU0ZXSg9gGWyo9jVSQ7iVCeccn3xgP76x+0S7l7JoyAAs\nkaIHYJeANLkRV+Oe947if77xnLN6LfGcToHgeJkEJDyA6WQeayI+GT+YrzMGIDqJblsTxthcpqSC\nWWz4vSEvusoK4Z58dQa/9i9P4D+fbvyXQngAqWUQVC33ADjnuOtHB2hYTw3yegGaUWj3MuomntGh\nGRzTyeVbDNmRBqDd3UDPBr/HjbBXOasYwGKJWpu7PbVTEM/qYAwIe0s9AAAYjPgQ9aslElBv0FMz\nBiDqAM5bE0FeL2AykcPnHzqM/eNx2fuoJ+BBd0AtMSq7j80BAP7fg680vB31uOUBdIqk8tihafzk\n5TOOPys3AFmtgH9++FXc/6Lz/QVnYlm8/Z8ek9faagoF3hTvrR5+70t7cOcPXm7Lay+GKavSfia5\nfIcidaQBaHc30LOlP+yVvwxAsSdPozl/bRQDYS/u+cWRii9pIqsh5FHgcpkVuV1+syIYAAYiXmkA\n5jN5eNwuDEZ8NRvLiVP2eVYB3Kce2I+/+/FB3PvYURkD6A6q6AmWegDPnZxDV0DFdDKPf33k1cZd\nPMwhNEDn5NZ/7ueH8JmfvuL4s4ymQ7He/0zesNVe1D4t7jk+ixfGYnj5VO05Es0gqxm47BM/w3ef\nac8Us2PTKZyca4/hWwyi1crMMm6H0pEGYLnRH/Ziyuq3k9cLyOmFBSWgxeBT3fjQr2zF7mNzeOSV\nqZKfxTOlcQeXi8n5BYPhogcQz2iIBlT5/2qkcjr8qlumqH7/OXPy1y+PzWI2nYfqZgh5FXRZdRCA\nqYk+d3Ieb9kxiBsvGMK//eJIQ2cSjNtqGpqRW//YoWn8r68/C71OGWIqkXMMyAPmqV9kb6VtBmDe\nYXqcnVPWBjhf47NpFkenU5hO5vDyAlPsmkUqpzd9lGkjEa3cp5fxWFQyAA3A7gEU20A03gMAgNsu\nXY+Rbj/+7scHS3T5uEPcQchAa6KmAYhnNMylNET9dRiAvIGg1421XX4pLd1+9SYcn0lj/3gc3QGz\ng2mPLQZwYjaNubSGi9Z14/2v34KsVsCTR2Yact2cc4zPZ+BTzV/ZRgeCHz88jdu/uBvff+40Ts9X\nSmxOTMSzVb2odN6QTf7Seb1uAzAmDEAbuqweslKG7RltrSSR05HTl08MQHgAqbyxLBITnCAD0AAG\nwj5MWrp8vKwlQ6PxKC780RvPwcun49h9bFbenshWyk4iEDxoSUAFbmbSdPlVRPzKAr2AdAQ8Cnyq\nG7971SZ8+tcvlBXLjx+elqfb7qBHNoQT6XAXrevC9qEwfKoLz56Ya8h1x7NmTyORetrIOMChiQRu\n/+JuqG7z6zCdWvhEl7J6LCVzekWLb8A0UKLJn10CWqhmQlRd14rPNIvDE+bgosk2nGhF88GczQN4\n5sQczsTaY4zqwa79z9TxO9OJkAFoAP1hL1J5A6mcXvQAvM3xAADgTdsHAQDP2vKPTQnI2QMYsCQg\nADg+kz4LD8B8vr+6cQfesnMNtg9FEPIq0Awu+xP1BFXZEO7ZE/Pwq26cOxiC4nbhgpEuPHvCOetl\nMpHFj20B1HRex9HpVNUApAiKNsIAzCRz+IP/3Curon95bBZZrYC/ufV8ANVdes65jD2ITZJz56yk\ndN7szKq4GNKaUVf/JcDmAbTBAAgPoJmjRKshCg/tEtDvf3kv/vFB5xhLJzBly/6ZWaaZQGQAGoC9\nGrjYCK55nba7gx6s7wngebsBcCg+G4x44WKQdQCAuQGJGEBWqz4aMpXTESxrFe12MYxu7AZQnIcs\nOpXOpfJ49uQ8do1EoVgn6YvXdWHf6bjja3zqgQN4/5f3Svnorh8dxLV//zDe9JlH8MUnjlUYgtPz\npQZgodz6QxOJqtf27Il5PPDSGbxwynz/RA3F+WvNpAOnoN7TR2bw1n98FL/6z48DgPT4AOfCvEze\ngN/jht/jLvEAaklAnHNpABYyFM1ASkAOWWbNRmSM2SWgRFbH8RnneRSdwHQyB9EFfbpKJtBLp2J1\nx5TaARmABiBO2lPJnHTdaxWCNYIL13WVGACn1NP3vnYj7v2dS+FV3NIDACA9AABVJ4yl8gYC3koj\ndulGc85xt9WgrscyABPxLPafjuPidV3yvhev70LeKFSMxIxlNNz/4jgAyMZuu4/NYnNfEF0BDz72\ng5fxqQcOlBgBoctvGTD7D9l7FZUzn87jbZ/9Bb7/rHM2izixi2uPZzWoboaRbrP5XrkH8J29Y7jt\n7qdweDKJF0/FZFqswCkOkNYMBDxuBDzukhhARjOqBjpnU3nZ5mKhWEGj0YwCjk2n4FNd0pttJeLz\nFO8N5xwZzZCZX53ITDKHDdacECcPYDyWwU3/9Bh+sm+i1UurGzIADaC/xR4AAFw4EsXpWBaT8Sw4\n52YMoMzoDIR9uGbbAACUGIAuv6fEI3AindMR8lZWKV++yTQAYuPvtjyBD3z1GeSNAi7f3CPve/F6\n01sol4F+8PxpZDXzVPTiqRiymoGDZxK4ftcafOv9V+K3r9yAf330CP7BlmI5HsvA7WLY0GMagFoS\n0NhcBprBq6bnidOmfUBOxKfCq7gR9ikVj3v81Wn0h73465vPR4GbOv1kWd1HOWnLAwh4FKTzRomm\nX03fF6d/F2u9BHR8JgW9wKWBb3UcICklIPP3QngCp+czHZHy68R0Mo9zB800aae40UwyD87bI6nV\nCxmABiAkoElbVkizsoAEF1kn7efHYkjlDRR4baNjjw9E/cqCBiBlBYHLuWCkC6/d0ovLrIH3Q1Ef\nGAPcjOHv33khrrUMDmAWoA1FfXj25DyeODyNO760By+OxfCN3SewYyiCjb0BvDgWw/7xOPQCx661\nXXC5GD7+9p24amsvfmh5CYBZBbwm4kPIusZaEpBIFxWbSTnJbPHkb/5dTKHtD3kr3PmpRA7DUZ+s\niTg+my6TgMzn+aOvP4tP3L8fRoEjrxcQUBX41VIJCKi+uQsDsKU/1PIg8KEJU/557ZY+AK2XgVJS\nAjKrpoUnoBd427KSFmImmcNIdwBBj9vRAxCHlIUKIl8Ym8fNn3+84YWT9UAjIRtAd8ADxcUwlczB\n7XKVVOQ2i53DUbhdDM+fnMfO4QgA1Cw+K/EAAh6bBFTFAOSNihgAYGYhffV9V8j/D3f58dM/fj1G\nugOOfY0uXt+FRw5O4icvn0FOL+DB/RMocOCvb96JXx6dxbMn5vHCmCkDXTBiavCMMQxH/TgylZLP\nczqWwVDUh4C1ploewBkrYFxNakk5egDm59Ub8lQYgOlkHmu7fHIs6IkZ0wNgzAwCCw9g7/E59Ie9\nskahKAEZsJ9hq8k7p+ZNvXvncKSizqPZHJpMgjHgCsuDm2pxdavY/AocclypYGwuI4cjNZqf7Z/A\npx44gFhGwwUjXbjnvaN1PS6TN5DKG+gLe9Ab8jpWA4vfs4U29hdPxfD8yXm8OBbDlVt6z/4ilgB5\nAA3A5WLoC3kxGc9VVOQ2C7/HjW2DYTw/Nl/RB8iJkFeRlcElMYCqeey6YwzAia0D4apN7S5e1414\nVsemviAe+pNr8KuvGcGG3gBuvnAtLhiJ4tR8Bo+8MoW+kBdD1gxkAHLjFMQzOroCHjnDuFbeddED\ncL5PotwA2OSz3qC34jQ3lcihP+xFf9gLv+rG8Zk0JhNZGTMQqb+zqTwm4zm5NhEEFllA4j2vluM/\nNpdB1K9ipDsgp7e1ikOTSYx0+7Gh15TYJuM5zKbyuPwTD+LJV81ajpxu4LM/O9SUnHf7JpnVjZKW\n36eaWB382OFpHJtJYTDiw88PTCBfZx2COCT0Bb3oC3kc+wGJa0rWmOMNADnL2L1ipeG2EjIADaI/\n7MXx2TSePjKL3pBn4Qc0ABEILu8E6gRjTJ5yIzYD4CQB5XQDmsERaoAX86uvWYv3v34zvvq+K7Cp\nL4i/f+eFeORPr0U0oMqsm4cOTuKCkWjJYHm/RynZaNJ5HUGvGwG1Hg+gtgEQJ7N4WQwAAPrCpR6A\nUeCYTeXQH/KCMYb1PQGcmE1hMp6TGUnxjIasZiCdNzCZyMpW2sIDyFhB4A1WVXUtCWik24+ugFmz\nkWxgtfP//q+X8Pc/rj5K89BEAucMhNEdUKG6GSYTOTx7Yg4T8RyesWo5nnx1Bp/56St46mhjivvs\n2IPO2bJAudNEukahGQWEfSp+57UbUeCoaH1eDWkALA/AKQtIeIILBdRFvOMgGYDly0DYi18encWB\nM3F89PpUJjKGAAAgAElEQVTtLXnNi9ZFEc/quOtHBwDUloCAogzUFVDlfWMOcoRoBBdwkIDOlt6Q\nF3/2tu0lg+8FwgBwXpR/BEGPG3mj2B0ylTezahS3OWqzlgEoDo5xPs2lbAPvAREDsCSgoBdzaU2m\n7s2kcijwYqB/fW/A8gByWN8TgMftQiKry3RWzeAyZTVgCwLHMpqUkJzec8Dc6NZ2+YvxGdv9ElkN\nD9hiImfL00dmsef4rOPPOOc4Mp3Clv4gGGPoD3kxmcjiJasfkdiARZ+ebBM8APsmmdMKJQagmZlA\nms6huhk29pmfzfGZ1AKPMBEn/r6Q6QE4JRwkrd+zxAIGQFzrwTNkAJYtAxFTvvj4zefLub/N5u0X\nrsVto+vw0mlTQ++zdQB1QhiAqF+FR3HBr7oRy2j4n197Fn/1/Zfk/USaZNAhCNxIIj4VG61TcbkB\n8Jdp/WlbUFqkVlZjIQ9AfCGFdFPqAZjvodjQpxPFLzoAbOgxDUAso2Eg7EXYpyCR1Uoa4h2dTlnX\noJTUAazt8kNxMcw7NIQTNQAj3QF0SamoaAD++4Vx/MFXnsGx6fo2qHJSeb2q0YxlNOT1Agat3+H+\niA9TiRxetFJ0RXB6zJoL0YyJbElbWm+uTAIaa6IEpBUKUN0ubLSkr2PT9XkAQvPvDXnRG/RiNpWv\nkOzS9UpAlgfwyplEyzuxUhC4Qdzx+s143Tl9eNuuoZa9pt/jxt++4wL8+Q3bcWLGPD3WImIzAOLv\nB/dP4NhMWma4AMVNN9jkQDZgegHHZtLYtbar5Hax2WfyBiI+BWmtGJQOqO6qmxnnfMEYgF0CymoG\ncnqhOEfB8lSmk3kMRHwyGCo8gA29AeQt72Ag7LMMgF5yAhSnyIDHlKxiGQ16gSPiV9FV1j5bIGYd\nmxKQuQa7PCcCzUdnUthozWI+G9J5Az7V+f2YLrvGgbAXJ2bSMj4kNmAhjzTDAJRKQAWpi6/t8jfX\nABgcHrcLPUEPwl7lLDwAywAEPegNeWAUOOYzWomnKyS8heZXiILFRE7H6Vh2we9xIyEPoEFs6gu2\ndPO3E/Wr2DWycOvsqF9F0OOWPW+ifhXHrEpL+wYmglcBhzqARvMbl6/H7VdvKplfAABBr/AAdGS1\nAjiHDEqLUzUA3POLI3ja1nBuPq3JE1U1AyBOZLGMJjdWER8RHoDo7SJyuIsSUHHz7Y94EfaplgdQ\n1ICPWqdIv2rGAHTrZCiC704xABHoXNvtLwaLbZ6C2ESOL9YDyOnyRFrOlOXl9IeKBuDoTArjsSyC\nHjdOWQOBxGzoZgeB7R7A1oEQTs1nmhYQ13TTA2CMYUNfAEfrrDyeTuYR9pm9soR3WJ4JlDpLDwAw\nvYBWQgZgFTG6oRtXWnneQNET2NwfxJzNhRUxgGZLQICZd/5XN+6ouN1vC/ambGmV5t8K0nndnLL1\n44P4WysGApS2jK5aB2DzAMQpu5gFJDyAXMnfdglIMBD2IuJXEM/qckgOAByzeQB+j73+QkVXwOOY\nBSSG/KyJ+NAVqJSAhMdzfPbsA6K6YbYoT1cxiMWAZrF3lMiGufa8AeQNs/JZeADNaNmcLPMAsjYD\nkNcLVVstLBXNKEBxm8kHG3uDZ+UBiN8JkfRRngmUdogBOEk8Oa3YPr7VgWAyAKuI37lqU0me8/ah\nMC7f1IPfuGw99AKXLn/5htsOhASUzhu2oHTRA0jnDcSzOvJ6Ac+cmJdfXNE0bjjqqy4BWdenF7iM\nF4gYQK88zZlf5qlEDgGPW8pha7v9Mp12MOJD2Fv0ANwuM9PqhHWKDHqVkvcw6lfR5XeWgETlrZje\nBpRKQCLmsZjeOGLjryablRu5gUjRG3vrTjOetf9MXK67WRKQx/JMs1qpBwAAY00KBOeNgvSIN/YG\nrSryhVNBZ5J52e1VegBl1cDCqAlP4Nh0Ctv+8kc4VLbJ53QD/WEv1kR8LQ8EkwFYxXz85vPxtfdd\nYfsFNjc98QvbiDTQxVIMAuu2oLTwANzIaEbJqfC/rIE1wgPY2Bd03Kg450hmdanVigwX4QFEfAo8\nbpfU/kUNgEB1uzDc5YPiMmchiBjAbCqP7oAHa6I+GSMQdQCCqF9FtEoMYCKeBWNAX8gDn+qGV3GV\nGgDLCFY7oWY1o2p9gXhsXi84NiabTprGSwSfRWX7xt4Atg+ZRYZPvVqU2TL5s2tuNpPM4eXTtce7\npnLFzySnF6T3Jg1Ak+IAuhUDAMz4jlHgddUdTCdz6A1aHoDwGstaPojf23TegFHgODyZRN4oVBiz\nnF6AV3Fj25rwyjUAjLHNjLF/Z4x9u1WvSSyMy8XkF0+cemUeewtiANUQMYBM3ihW1nrtWUCG/MIF\nPG58/7lT4Nw80btdDOu6A44SUE4vQC9wDHeZGS9C1ohaaaCMMfSGPCUegNDGBRt6gugLeeFyMSsG\noGMmmUdPUJWZNIAZrK70ADyOtReTiSx6g17ZSdUMFhc3dHF6Pznr3Bvnb390ALd8/nHH99IehBTe\nwHgsIz2+6UQevUGPLF4cCJvXsHNtVBa72Qf7nK0H8C8Pv4p33/1UzQyXZE6XUoq9DmCrVWvRrGIw\nzShAVczr3mQF148uIAOJRIM1VuFiV8ADt4tVSED2hoXJnI5Z6/PUyorNTAPgwrY1YRyeSra0e2hd\nBoAxdi9jbJIx9lLZ7dcxxg4yxg4zxj5a6zk450c457cvZbFEcxBfPBHIFMHCVsQAqhFQzddO5Y1i\nVpItBpDJG/IL9+uj63BkKoUXT8UwHstiMOxF0KuUDBcRCLd82GotIAKb9hqKPlthz3QyVxGgvv3q\nTfjQG7eaj/MrSOZ0TCdz6Al65ObpcbuguF0ylgGYBqA7oCKZ0ytkhsl4Tp68AVQYCrGJ540Czjj0\n6Xn44BSOzaQdW2Dbg7bi3791z9P41ANm7GTKpmcDwJBlHC9YG5VBTtG1NeJTzjoGMJXMIV6WKQUA\nvzg0hZ9YMyFSOUOuQcQAGDMN4UDYi4NnmjOmUjMKUFzCAzANwEKB9qlkDsmcLg2G28UwEPZWfC72\nzKZUTpeztPUyA57VDHgVFzb1BZHXnT/fZlGvB/AFANfZb2CMuQF8HsD1AHYAeDdjbAdjbBdj7Idl\nfwYqn5LoFIQrKzbUVE4HYyjZvFpNseWDLk9SfpsElMrrmLKahP32lRvgUVz43M8PYzyWwZqoDz7V\n5XhSFV/KYSvVrlwCAlDqAZRtjoAZGP3NyzcAKDb9OzGbQW/QK/VzsVa7BCTSQIHKCuyJRBaDNu09\nWhYrSOcNKVWUb1AT8aysPZiIVe9JY//3RDwn5YbpZK6khqQv5MVXf+9yvOdK8xrX9fjNZoNeBWui\nvgWzgLKaUdLWQFzribIA9r88/CrusqqTUzldSilZzRyx6FfdYIzhNeu7sed4YybLlZM3uIwB9IU8\nCHrcODaTxtd+eQLf3HPS8TGiR9UmWzruYMRXMb0sbV0DYB485qzPs9z45/QCfKobayzvcSLeuj5M\ndRkAzvmjAMrLCC8DcNg62ecBfB3AzZzzFznnN5b9max3QYyxOxhjexhje6amWtsQa7UiJCBRzJTK\nGwio7qb3M6pFMQ20KAEFy4LA08k8XMw8uX3krdvw030TeOrIDIaifvhUM/2y3J0WHoDItT45l4HH\n7YJXKX4V+qzmXnm9gPm0VuEB2BHZG9PJHLqDKgat+9ozlgBz83S7GKJWjn95HMD0AIryUTSglgWB\nDamHHysLBD9lk2dEENyOPfibzhsoFDiSOV0WlU0ncjKgKXjt1j659pFuM/NppCdgtuhYwAP4whPH\ncOPnHpOegmi5cbLMAMynNZy2UjyT+aIElNMLyOqG7C81urEbY3MZmSnVSDSjAI8lATHGsLEviK8+\nfQJ/9t0X8W+PHnF8jDC2m/uLBmAo6qs4uSdzujTqiazNAzBKPYCc5QEMSgPQeR6AE2sB2E3kmHWb\nI4yxXsbY/wfgYsbYn1W7H+f8bs75KOd8tL+/fwnLI+rFo7jMPviW7HE2jeCahU+xp4GWxiQCqoK8\nXsBEPIueoBduF8PtV2/CG88bQIEDa6I+efLKlumtIidbeABTiRwifqWkD1Gv1dyrvEDKCfsQnp6g\nV36J7d4KUPQwumSGTx4nZ9MwLCM1ncyVeABd/nIDoGNzfxAetwvHZ0s9gKePFs9mTvKBPQaQ0Ypp\ntTOpPOJZDdPJfEWcw46IA6zr9sNfxbOyc/BMQhpP81otD6DMcMUyZvHbeDwLzs33DxAxgIL8DEet\nGQV7jjXeC9BtWUAAsG1NGAbnWNvlr9rD58hUEl7FJWVEwPyds3sAnHOkcrrsEJDK6XIedLkHkNcL\n8Kpu+fkvFwNwVnDOZzjnv88538I5/2SrXpeoj76Q15YF5NwKupW4XAx+1Wz5UB6TEJvqybm0PLky\nax7B6IZuXLW1Fz7V/NUulyvE5rfG1nm0vIfSlv4Q8kYB331mDABqbo72uQ+9QY+UgMQaxSYmpB/x\n9xefOI7X3fUQvvPMGGZSebPfkC2A7CQBhX0q1vX4cXy60gMQg3rE5LR/+vkh2d4jbQtGpnJ6Sc79\nS2Mx5I1ChcxlRxqAngD8qnvBGMAR64QsNjzRcqNcAhJBaFH8FPYp8Cgu2Q3Ua32GO4cj8Kmuqr2M\nloJmk4AA4K9u2IGH/+QavGXnYNUePkenU9jUFyzxkIeiPiRtM8HzhplsIA4ESbsBKIsBiCBwT9AD\nj9vVkTEAJ04BWGf7/4h1G7EM6Q0Wde9UTm9JG4iFENk+QsIQm6k4XZ+YSZeczruDHnz7D16LXzlv\nEF7hAZRtVqLnTNSvyJkN4bI22jdfNIx1PX589ueHASzkARQf220LAosgtjAEshGf3zRYP3jeTFt9\n7uQ8Ji3Nd9AeBA6oyGiGDOqavZDcZrGSbSOdTGRxZCqFXzlvABGfImch3P/iGTlToMQDyBsllalC\nW691jessCWhdt7+kClvAOZcZS5xzHJ0yh8uUewD2dRsFLquwRbwg5FXgVVzIaQXktKJ+rrpduHCk\nC3ubEAcw6wCKG3l30IN1PQGEvWZw3ylz6chUqkT/B1Ah34i41RrrQJDMFRsGlsuSOd2UgBhjGIh4\n5e9DK1iKAdgN4BzG2CbGmAfAuwD8oBGLYozdxBi7OxarnTtMNI6eoMcWA9DbmgEkCHjdMg3Ub4tJ\niE11PJ6tejoXm0d5VozY/EJetST3345XceNP3rJNVsPWarJnb8Ft9wD8ZTEAYQC6gyoYA3atjeLC\nkSj2j8flpmFPIY3a+gFxzmUvpPW9ARydTuIT9+/Hx+97WbZ4vmJzL4aifpyOZVEocByZTsqNtzwG\nYD/Z7j5mnqpreQA7hiNY3xPApZt64FPdFRLQz/ZP4rJP/Ayn5zOYTeXliT+WySOrGfJ9tMcAErY5\nFKL6Neg1WyuIVhD2GROjG7vx8ul4zSaAi0Erk4AEIZ8CziuL5zSjgBOz6RL9H4AcWCPqUIR8JD2A\nrC4NYmUMwKwDEPcvDyY3k3rTQL8G4EkA2xhjY4yx2znnOoAPAvgxgP0Avsk5f7kRi+Kc38c5vyMa\nXbi/DdEYekNeWcmYzhttrQEQBFQFqbxuTiezrUcYAM6rb85i8ygvWhJfzKDXLTdlp0E6N10wjB1W\nEVR5gNSO3QB0BzzwKm50B1S5Rp9qTogTrxX2qfjK7ZfjP3/vcrxmQzcOnklg3DIAA2VZQIDZElr0\nQvJ7FFyyoRtZrYAvPXkM39h9Et/cM4a+kAc7hyMY6jI3j1PzGWS1AuJZc6iMXctO5/USD0DMa+4L\nV7/GvpAXj37kWuwcjjpKQEemk8jrBew+NisDpIDZ4E7IPH0hM01SPNYe33hFGgA3fKrLSgMtlGSh\njW7ogVHgeO5k6Xzps+XRV6Zwy+cfl6dw0QuonJDXfP/Lp3mdnE1DL3Bs6guV3C6GGUkDYBkqEQNI\nZO0SkEMdgCV3rYn4WhoDqOuYxzl/d5Xb7wdwf0NXRLSFXssDKBQ4YhkN62w9b9qFyPbxl80ntv+7\n2uYsYgDZMg8gYYsniBkATnMUXC6Gz9x2IZ58dUaezpwoiQFYa3nHJSM4xxoWzhjDpr6g/D9gZtgA\nwPahCNJ5A3uOzVpVwKVBYMAcHtMdLBqtGy8Yxlt3roHqdlnSiwYXY1DcLgxFfXjpVByHLQlGjKtM\n5w2obgbN4EjnDbmp2TuT1vIA7IgZx3ZE+vBzJ+dLGpvNpzWZAbRrbQQPHZzCqfkMtvSHSgyAmEcc\n8irwKZYHkDfQHSi+t69Z3w0A2HtsTs4tXgxPH53BcyfnkcyZE+a0Aq/qAQDm+zcYKd4uDFy5BCSM\n95kyDyDqV+FVXBiPZSCkf00vegCFAkfeKMgstIGIFw8f7DADQKx8ekMeFLjZyOz4TBrvvGSk3UtC\n0JKAUqpRUlFr/3c17dpfJQaQyukIekw5qegBOH8NzlsTwXlrIo4/E3gUlzy1dluyzV/cUNrc7mcf\nfoPjY4WH8egrU+gNeko2IlkvkNaKIyZtmjhgGpduW/vhNRE/ppM57B8vFk3FMppsszARz5kGwPIA\ndq2N4heHpuFikGtfCL/VhoNzLjOnRLbUcyfn4VfdUFwMLmbOPYhZ0+rOXxvFQwencGI2bQ291+U1\nCUkp5FXgFR6AXioBRQMqzh0MLbkeQMx3yOkFcM7NNFB3ZbqziA+VewCiBmBLmQTkVdzoDXpkADcl\nGyq6EfYpJQFw3eYBCIMprnVNxIdU3kAiq5UcLppFR/YCohhA6xG1AD/ZNwGgmHrXTvyqOU0rky81\nAPbiqmon16IEZH4R7Y25RIBbnPwXmqS2EGGfirDXzGBxgjFWkmYq2DoQguJimEtrJTUAAGwtobVi\nL6QFAvOigveJw7b22Jk80nkDIa8is6qELLNz2JRYRSptPfhUNwocst8RUGwh8vLpOF6ZSGB9b8D0\nLlJFD0BMfxNxAOEBnDdU9IyEB5DVDGTzRsWc6Us29OCZE3NLag0tejzl9QKMAgfnkO037BQ9gNJ6\njSPTKXQHVDmzwY49FbQoNSoIepWSUZOaLQYgYlTCAxhscTFYRxoAigG0HrGR/uilM1DdDBet61rg\nEc1HTP5K5UuzkkoloGoGQEhABYzHMrj4r3+Cxw5NI5HT5Ze7VgzgbAj7FPQsYg60T3XLucJ2/R8o\nZguZJ/j6RnQKHfqXx2alMYpZBkR0JrVLQOevXTjGUY70rGyxlZlUDoqLIa8X8OihaWzuC5oGIJOX\nxmZLfwhexSVrAYQBEM3mAHsQuICsXqioRB/d0I1EVscrk4tvmCa8lZxekBuxcwzA8gCy5R5AEpv7\nQxX3B8z3vxgDKHo1Ia8i03OB0iwg4QHYg8BA62oBOtIAEK1HeADPnZzHLqsHTLsJet2yHXQ1CWgh\nDyCrGTg5m4FmcPzy6AxSOV1+uaNVsoDOlohPdZx5XA/brRPwYJkHEPYpYAyIpfPSiwkskJklMlHy\negG7rBP3fFqT75+IqSSzZkrpZiuQWSsFtBzZosMmrc0k87h8c4987U19QWvuQXHeQtSvYn1PQEoh\n5QaAMfNz9Sou2QpCGHHB6EYzDrB7CQVhooFgXi9IL0Z1kIDE74g9Y0ozCnj5dBzbbNPz7AzaArjC\nAwh43Ah5lZIGfvZCMDH5THgAoj6FDADRUnptp8BLN7Vf/gFMCShjDYSxp6WKTcjFUHXjtRsAsdns\nG08gmS0+V6RBHsAHrt2KD167dVGPFRtguQfgcjFEfGqJBLSQB2Avbrtkg7lZSg/AoyBoDdJJ5nSE\nfYochF5vABgoegDCAHDOMZPM4/y1UdnMblNfSM49iMuBO0qJAYhnNahuJrt9Bj1mNbbPyjLK6kaF\nB7C+J4C+kBd7jy2uIIxzLgPWOd2QJ3En6U5kd5XUTBybQzKn4w3nOncoGIr6MJsyU1+TNgnI3lbd\nq7hKCsGkBKQKCcgKJq9mA0AxgNZjDwJeuqEzDEDA40ZaMyrSUgPWxlBLu7YbAFGktH88jqSDBBRd\nogF4845BvHH74KIeu2NYGABfxc+6rH5ARQ+gtgEIeRW5cYmsGdFuIeBVpAeQsLyggEfBm7YP4Mot\nvXWvtzy2ksjpyBsF9Ie8UjbcZJOAYhkNPtUFr+LGup6AbOscy2iI+lVZZSw2Sa/qQjyrg3PIYj4B\nYwyjGxbfGC6e0eWpP2+TgEQ3UDtBhyDww69MQnUzXLXVOQtpjeWBTcSzSOd1KC4Gr+KSv2+Ki6E7\n4KkpAQU85mfYqmKwjjQAFANoParbJTNPhKvdbvweNwwrLdUufyhuFzxuV03t2qeI6VIF6QGcms/g\nTDwrN5tLN/XgTdsHce6gs0vfCl6zvhtv3jGIqx02FXGKrjcIDBTbXO8cjsihMiLzKWCTgEJW4Pue\n916KXx9dV+spSyiXgEQAuDfkwejGbjBmZsh0WxJQPKNLAzsU9SGRM4PQsYyGiN+cn8BYsfmfV3Ej\nZqWmOnWjXUpjuCnbAKG8UZBSjJMEpLrN7K4SA3BgCqMbeqoOShLdPMdjWaQs2Y0xJj+37qAHqsJK\nCsHKg8BAa4vBOtIAEO2hN+jBuYMhxwyHdiD6ERkFXnH69XvcNbVrxe2C6mbI2CQgwNTExRd4bZcf\n97x3tK2Tz4JeBf/226MVeeWAKU3NZzTbSMyF4zKiFfbaLr/pQaQtD8CjWLOUTXkivMhrLk+vFQ0E\ne4Ne/PaVG/HN91+JgYgP0YCKnF7ARCIrs6xEA77x+SziGQ0RnwqP4sJg2Cc/A5/qkqd0pziUkLZE\nY7h0XscdX9qDw3UEhqdsE7tyWjEGUC17K+RVZbuK0/MZHJxI4NrzqjeotOv39liTeK97Ah6oLldJ\nBlV5DAAwDUmrJCCqAyAkf3jN1o7oASSwn/rLW1P0Bj2ypXM1REqhbnC4XUwG4jrpGmvRFfBgbC4j\n2xEsFAQGgOvPXyMblUX9KubSeSsLyPQAMnkdhQKv2eCuFv4yCcg+T9inunGplT4sJMUTM2kZpxEG\n4PR8BrGMJu+zdSBkq5y2p/tWbsw7hiNgDDg0mQAwhP3jcfxk3wRCXgWfue2immufruoBOBuAiE+R\nHoDoq3TNtuqjTUQW1omZNFK2jrrCEHQFzM+j1AOoNHYDES+OvJqseS2NYnl8E4iW8GsdUPxlx57v\nX96a4p73ji6o3fs8bmS1ApI5HSPdfsQzGubSGkId0OaiHkwJKI90XodXcdWVq/+uy9bbHu/BRCIH\nzmF5AG6k8gY0g0td+mwRm7KQgERQtVyOE5XMJ+fS2Gh5N2IM5+lYBvGMho3WBK7/966L4LLqJOwn\nYZ9DBbZXcaM/5MVpa66uSK/84Yvj+Ksbd5QUxpVTYgD0gtyIqxmAkE9B0kpjfeTgFIajPpwz4JwC\nCpgHi60DITx7ch56gcuDhvi7J+hBIquXFIIJT8qrlnoAk4kcCgXe9JkcJAERHYu9/0+5B7C5P4Te\nBU6xZoWuKQF1BTwy46adks/ZELVmAiStTqBnS8Svyo3S9ADMrKpEVlv0eyCCleUxgPKNN2rFkzSD\nS0M9EPbB7WLSAxC394a88vH2k7CvyjUPd/llvr24vrxewLf2Ok/wEtglIHsaqOIQAwDM3xPhARyc\nSODi9d2OBX12Rjd0Y+/xOSSzxYOGMLZmDMBVVghWGgQGzLjQrRevLWmr0Sw60gBQFhABmGmg8t+L\n2ACFBBRL59HlV6UBWD4SkIoCByYTubrkH6fHi1Ov8ABEGuhiax/E5yBjAKkcugJqxSnanlUmXsvt\nYlgT8eHUXAbxrO7owfkW8AAA05M4ZW3847Eswl4Fl27sxleePoHpZE5mfZUznczJgG9ON+Rwdk81\nD8CrIJE1W0JPxLMlabbVuGRDN2IZDfvHE/IzE8a2O6BCdbGyVhCVQeA37RjE373zwkX9zp8tHWkA\nKAuIAEqDnotpT+33mAZg3jptnmcV8CwnDwAwT7mL8QCifhWinX3QKgQrcKDAsXgJqCwGMJPMy1m+\ndrpsjdzsG/1wlw+HJpMwCtyxB1OJB6A6b0/DUT9Oz2fAOcep+QyGu/z4rSs24PhMGqP/90Fc/H9+\nWjKTWDCdzMtiuYUqgQFLAsrpSOTMhnqDkYXjJqKFSkYz5O9Z0QB4oLhZSTO4ogfQnq24Iw0AQQCl\nEtBi2lP7FLfMAuoKqLhicy/WRHwlnTk7GbFxjseyixrR2WXbeANepWTKm2h3fLb4ygrBppM5RylO\ntLIASgvthrv8svunkwdg18KrnYCHu/zIagXMWTOFh7p8uPGCYXzyV3fh/W/YDM4r5w8DpgQkEgcW\nSgMFIIfCTMQq5zVUY2NvQBrEYLkEFDAb/tnbQcssoDZV3pMBIDoWf40soHrwqi5k8pYB8KtY1xPA\nU3/+RjlcvdMR6bizqfyiRnRGbadwsw6g+B4u1gNwuxg8SnEu8Ewq71iP4bfaOgCVBkBo784SkNvx\n33bs2UTjsSyGu/xwuxjefdl6WdNQ3sUTMI2VaJiX0xbOAgr5TAlIpGSuqcMAMMZkqqr4nT1nIITX\nndOHyzb1QHEtXAfQSsgAEB1LwHYqWowE4lfdmLKyYJba7qEd2DfIxUpAxccrJV7UYusAAPN9FSfX\nmWQOvUFnaUTIQPZuq8O21F2nz6Q0DbR6DAAAXp1KYjaVx7BNmxeV0PGyJm5mG4gcBsI+qG5meQAL\nSEBeFUaB45g1A6CeGABQLKQUsaawT8WXb78c63oCpgdQVgnsYmaVcDsgA0B0LCVpoIsJAqtuTFiZ\nH51S3HY22HX0xQSB7QZA1AEIFusBAMWhMLphyjC9VSqyhQxk1/rtm7WjBFRXENg0Is9YLSHsRiUs\nJnmVGYBYRoNmcPSFzKltZiuI2hKQeI8OT5qSVT0SEGC2rQacf2edDIBXcS+YXdQsOtIAUBYQAaAk\n930xmTs+1SWLv7rIAyjJqlpKIFwMhZlNizYQtT2AqN/ZA3COAdjTQJ23p96gBx7FJbuC2p/Tp5q/\nM+5JJuMAAA8pSURBVOV9/EU2VH/YC4/iQk43bN1AnV9HeEmHp5LoCqh1d8i9YCSK37x8Pa7ZVlk1\nrLgZdHszOK2y62kr6UgDQFlABGDqqQHVDRdbnEZq7yVj18OXCz61qKMvLg20eDIPet0lQfWlGAAx\nGF5M1+qrUny1OAlITDurnp7JGMPaLj8OnDEnn4n+R+JnYVsFr2DKWmt/yAuP21XiAVRvBWG+R69O\npurS/wWq24W/uXUXtg5UJhsoLldJDCBrGwjfDjrSABCEwO9xy1bBZ4v9xLYcPQCguIkGF5EFJU7Y\njJlyit2LWMoUNL9VYDeTsvoAVfEARC2A3fhGfGY2kosBIQejJjZDv1pbFhnu8qHAzWsbjJa+vsjf\ntyMawfWFvfCqrrorgQGzNbNTt9bF4FFYmQRklGQ+tRoyAERHE7TaGC8G7zL3AICijr6Y90AUYAVU\ncwZySVbVEtph+D1mDEBU4VY7HfdZp237Rs8Yw3CXHxG/6tjmQHgAC8ktIp+/L+StOEGHfWqFAZhL\nmR5AT9BjegC2NNBalcCCNXXUANSD4nKKAbRvG14eFTHEqsWpJfBiHrvUnv/tQqx7MWmwituFsFeR\nLRVEKqlfdTvOwa0Xv+rGfFrD4ckkvIoLa7udm/L9zlUb8bpz+io2ensqaDli41/ocxdS0rBDQ8Cw\nV6mIAcjBNFYH0pJuoNViAD67AWiMB6C4y9NA2ysBkQEgOhqzp/riHitOk37V3dYv2VIQnstivaBo\nQJUphuI5lpIBBBRjAIcmzfm41ZrU9YW8jtPG/uCaLbKHkNNzA1hQFllrpYIOO6Rmhn1KRTvleNYc\nTONRXPAqlgegL5QGWnyfButMAV2IikIw3SAPgCCqcdG6rpL5s2eD2Ey6lqn8AxRjF4vxAIDSdhAe\nt5khs5QaAMA0qNm8gcOTSTl57Gy4YnP1CWRiM1yKBxDyKUhMlkpAiawu4x5mFpApAbkYqhqwUBM8\nALXcA9AKbY0BdKQBYIzdBOCmrVsXN2eVWDn85Y07Fv1YsYksV/kHKK59MWmgALCxL4i81W+GMWYO\nKV+iB+D3uDGX1pDVjbOaJlYPqmWkFooBiI1/qIoHUJ4FFM9qMuvIo7jNuoBCoaYU5lXcMl5Qbw3A\nQiguF/QCB+ccjDHk9EJbixQ70gBwzu8DcN/o6Oj72r0WYvkiJKDlbACE97JYA/D377iw5P8Bj3vJ\nzfD8lgQEoCltNXyKa0EPYHNfEH92/Xm4+aK1FT8zJ3lpcpMFzHnAQtP3KlYaqM6r6v/yuXwKZlP5\nhhkAUXSmGRwehSGnt7cOoCMNAEE0Au8KkICiAdFYbGntmwVBr7KkFFCgNEOn1oCUxeJV3Qtuiowx\nvP8NWxx/FvYp0AyOnF6Qa01kNVkX4VFcyOsGNKNQtQpYELICyk4dTxeD8Dj0QgEeuCgITBDNYiVI\nQFv7Q+bc3AadQO+8aWdJr/7FIIyK28WwobdylvFS8SmuuqtunRAn/URWl88Tz+pYb63V6y7GAKoF\ngAUhr4KBsK9hk7nE64k+RFmNgsAE0RSKQeDl1wdIcOWWXrzwsbcsaUO08/pzqw81rxdhWDf0BqpW\n0S6Fd4yuW5JnIQxAMqejP2xmIcUzmrzdY0lA+ToMQF/Y6zi3YLEIj0O3UlCpDoAgmsRKiAEACxdF\ntRphALb2N6et9offfO6SHh8qawjHOS/JAhJpoLrBF5SAPnHr+UtaSzmKq9QDMLOASAIiiIYTsJqf\nLecYQCci0hbPGezMuQpFCcgs/spZp31xkhceQD0S0Eh3oKFrU2QQuADOedvrAKgVBLFiWdfjx1+8\nbTvedv5Qu5eyopAeQIcO1hFZTgkrFVRUAYcd6gAWMgCNxiODwBx6gaPA2zcMBiAPgFjBMMbwvtdv\nbvcyVhxbBkLoC3kwavW97zSE1CP6AYnhMBGZBuqGUeDIagWoLd58FVsMoDgPmCQggiCWCVv6Q9jz\nl29u9zKqIgrdkpYEFLf+LhaCmZt+MqfDs0AMoNGIGEDeKCBn1VLQPIAyaCAMQRCLRUpA2VIJSLaC\nsGSYVE6XG3KrKGYB8Y7wADrSANBAGIIgFoto+CbaQSTKJSC1aABaLwEVC8GkASAPgCAIonGEfYrU\n/iskIHf7JCB7K4isJQFRFhBBEEQDCftU6QHEM8IDKI0BpPJGy7OAipXAnREEJgNAEMSKI2QbCpPI\nalBcTAZbxYZrFHjLDYCYzaAbXAaBKQ2UIAiigYR9iqwEFq2gRWdQ+4ZbbRxksyj1AKz1UAyAIAii\ncdgHw8czugwAAyjpX7RQO+hGo9oKwTpBAiIPgCCIFYc9BpDIarIKGCj1AFouAdlaQRgFsx8QzQMg\nCIJoIGYWkCgE00s6enraaABUWzM4o2DGAAKLHPfZCEgCIghixSHGQnLOEc9oJUNwSg1AiyuBba0g\n0nlhACgLiCAIomGEvAo4N1M9E9niOEigVPdvWxpogdsMAHkABEEQDUNo/smsbmYB2WMAtv77rTcA\nRQ8gldOhullThurUCxkAgiBWHKIh3Fw6j3TekFXAQJkHoLRaAiqmgabzRltP/wAZAIIgViAbesxB\nLg8fnAKAUgmojWmgohBMMzhSOb2t+j/QoQaAuoESBLEULhiJ4tzBEO59/CgAlEpA9kKwBg17rxdZ\nB2BwpDWDDIAT1A2UIIilwBjDb1y2HlOJHADUkIBauwW6XQwuZnYDTed0BL0kAREEQTScWy8ekad9\nuwTkcjEZjG11EBgw4wB5o4BU3pDjNdsFGQCCIFYk0YCKGy4w50HbJSCg2H6h1TEAAFBdzJSA8u33\nAKgSmCCIFcsfXrMFqZyOzf3Bkts9igvItccDUBWXLARrdwyADABBECuWrQNh/Ot7RituFyf/VncD\nBcy5wFqBI50zEKQ0UIIgiNYiWjC3RQJyM7MQLK/DT1lABEEQrUVs/O0JAjNohtkKIuglA0AQBNFS\nRDFYq5vBAWZH0FROh1HgVAlMEATRakR6qNIWCciFWMZsVd3uIDAZAIIgVh3CA2hHDEBxM2kAKAhM\nEATRYjxWHUCrm8EBptchPQCKARAEQbSWdgaBVRdDnDwAgiCI9tDeNFAXUtYwGEoDJQiCaDHedhaC\n2V6TPACCIIgWU0wDbY8HIKAYAEEQRIvxttEA2GcQUBooQRBEi2lnGqh9BgEVghEEQbSY9lYCd44H\nQN1ACYJYdVy2qReHJ5Nwt3gkJFCsPvYorrZIUCVradULMcZuAXADgAiAf+ec/6RVr00QBGHnDef2\n4w3n9rfltYXX0e7TP1CnBMQYu5cxNskYe6ns9usYYwcZY4cZYx+t9Ryc8+9zzt8H4PcB3Lb4JRME\nQSxfxKm/3SmgQP0ewBcA/BOAL4kbGGNuAJ8H8GYAYwB2M8Z+AMAN4JNlj/9dzvmk9e+/tB5HEASx\n6lBcpgHoBA+gLgPAOX+UMbax7ObLABzmnB8BAMbY1wHczDn/JIAby5+DMcYAfArAA5zzZ6q9FmPs\nDgB3AMD69evrWR5BEMSyYdlJQFVYC+Ck7f9j1m3V+BCANwF4B2Ps96vdiXN+N+d8lHM+2t/fHo2O\nIAiiWSjSACwfCWjJcM4/C+CzrXo9giCITkRIQO2eBgYszQM4BWCd7f8j1m0EQRBEFUQNQid4AEsx\nALsBnMMY28QY8wB4F4AfNGJRjLGbGGN3x2KxRjwdQRBExyBaQSybGABj7GsAngSwjTE2xhi7nXOu\nA/gggB8D2A/gm5zzlxuxKM75fZzzO6LRaCOejiAIomMQhWCd4AHUmwX07iq33w/g/oauiCAIYgUj\nsoCWewyAIAiCOEvUDvIAOtIAUAyAIIiVyrKLAbQaigEQBLFSKXoAZAAIgiBWFYqMAZAERBAEsaoQ\nHkC7B8IDZAAIgiBaiswCoiCwMxQEJghipXLZpl68//WbceG69sc4Gee83WuoyujoKN+zZ0+7l0EQ\nBLFsYIzt5ZyP1nPfjvQACIIgiOZDBoAgCGKVQgaAIAhildKRBoCCwARBEM2nIw0AVQITBEE0n440\nAARBEETzIQNAEASxSiEDQBAEsUrp6EIwxtgUgOOLfHgfgOkGLmc5QNe8Olht17zarhdY2jVv4Jz3\n13PHjjYAS4ExtqfeariVAl3z6mC1XfNqu16gdddMEhBBEMQqhQwAQRDEKmUlG4C7272ANkDXvDpY\nbde82q4XaNE1r9gYAEEQBFGblewBEARBEDVYcQaAMXYdY+wgY+wwY+yj7V5PK2CM3csYm2SMvdTu\ntbQCxtg6xthDjLF9jLGXGWN/1O41NRvGmI8x9kvG2PPWNX+83WtqFYwxN2PsWcbYD9u9llbAGDvG\nGHuRMfYcY6ypA1FWlATEGHMDeAXAmwGMAdgN4N2c831tXViTYYy9HkASwJc45+e3ez3NhjE2BGCI\nc/4MYywMYC+AW1by58wYYwCCnPMkY0wF8BiAP+KcP9XmpTUdxtiHAYwCiHDOb2z3epoNY+wYgFHO\nedNrH1aaB3AZgMOc8yOc8zyArwO4uc1rajqc80cBzLZ7Ha2Ccz7OOX/G+ncCwH4Aa9u7qubCTZLW\nf1Xrz8o5vVWBMTYC4AYA97R7LSuRlWYA1gI4afv/GFb4xrDaYYxtBHAxgKfbu5LmY0khzwGYBPBT\nzvmKv2YA/wjgIwAK7V5IC+EAHmSM7WWM3dHMF1ppBoBYRTDGQgC+A+B/cc7j7V5Ps+GcG5zziwCM\nALiMMbai5T7G2I0AJjnne9u9lhZztfU5Xw/gA5bE2xRWmgE4BWCd7f8j1m3ECsPSwb8D4Cuc8++2\nez2thHM+D+AhANe1ey1N5ioAb7c08a8D+BXG2H+2d0nNh3N+yvp7EsD3YErbTWGlGYDdAM5hjG1i\njHkAvAvAD9q8JqLBWAHRfwewn3P+mXavpxUwxvoZY13Wv/0wEx0OtHdVzYVz/mec8xHO+UaY3+Wf\nc85/q83LaiqMsaCV2ADGWBDAWwA0LbtvRRkAzrkO4IMAfgwzMPhNzvnL7V1V82GMfQ3AkwC2McbG\nGGO3t3tNTeYqAO+BeSJ8zvrztnYvqskMAXiIMfYCzIPOTznnqyItcpUxCOAxxtjzAH4J4L855z9q\n1outqDRQgiAIon5WlAdAEARB1A8ZAIIgiFUKGQCCIIhVChkAgiCIVQoZAIIgiFUKGQCCIIhVChkA\ngiCIVQoZAIIgiFXK/w86zrCC+8gEigAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<matplotlib.figure.Figure at 0x10d707ef0>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "x_axis = np.linspace(0, 5, len(losses), endpoint=True)\n",
    "plt.semilogy(x_axis, losses, label='adam')\n",
    "plt.legend(loc='best')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "可以看到使用 adam 算法 loss 能够更快更好地收敛，但是一定要小心学习率的设定，使用自适应的算法一般需要更小的学习率\n",
    "\n",
    "当然 pytorch 中也内置了 adam 的实现，只需要调用 `torch.optim.Adam()`，下面是例子"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 5,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "epoch: 0, Train Loss: 0.359934\n",
      "epoch: 1, Train Loss: 0.173360\n",
      "epoch: 2, Train Loss: 0.122554\n",
      "epoch: 3, Train Loss: 0.100869\n",
      "epoch: 4, Train Loss: 0.085850\n",
      "使用时间: 93.85302 s\n"
     ]
    }
   ],
   "source": [
    "train_data = DataLoader(train_set, batch_size=64, shuffle=True)\n",
    "# 使用 Sequential 定义 3 层神经网络\n",
    "net = nn.Sequential(\n",
    "    nn.Linear(784, 200),\n",
    "    nn.ReLU(),\n",
    "    nn.Linear(200, 10),\n",
    ")\n",
    "\n",
    "optimizer = torch.optim.Adam(net.parameters(), lr=1e-3)\n",
    "    \n",
    "# 开始训练\n",
    "start = time.time() # 记时开始\n",
    "for e in range(5):\n",
    "    train_loss = 0\n",
    "    for im, label in train_data:\n",
    "        im = Variable(im)\n",
    "        label = Variable(label)\n",
    "        # 前向传播\n",
    "        out = net(im)\n",
    "        loss = criterion(out, label)\n",
    "        # 反向传播\n",
    "        optimizer.zero_grad()\n",
    "        loss.backward()\n",
    "        optimizer.step()\n",
    "        # 记录误差\n",
    "        train_loss += loss.data[0]\n",
    "    print('epoch: {}, Train Loss: {:.6f}'\n",
    "          .format(e, train_loss / len(train_data)))\n",
    "end = time.time() # 计时结束\n",
    "print('使用时间: {:.5f} s'.format(end - start))"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
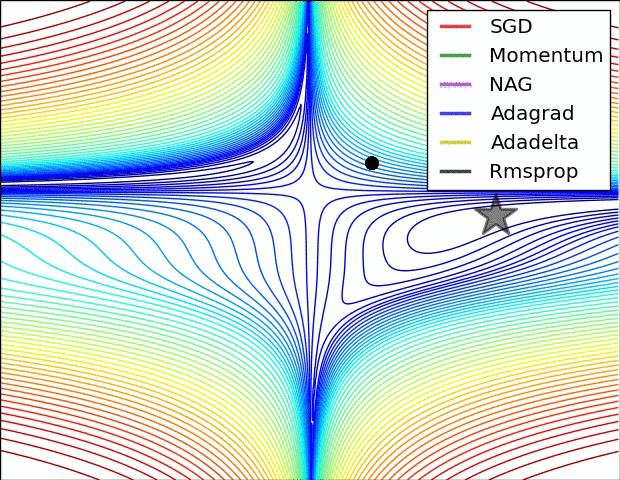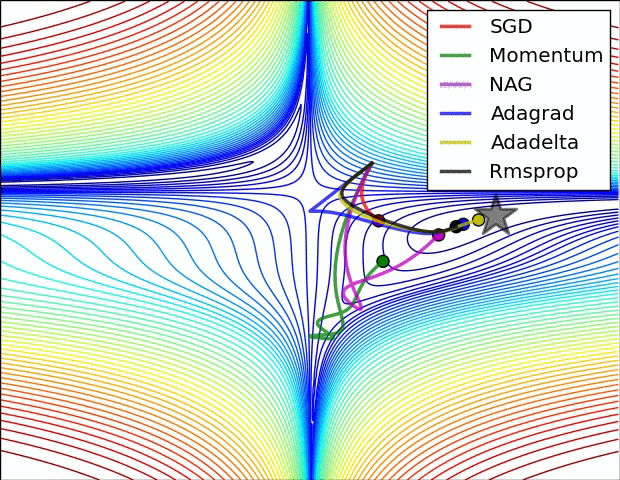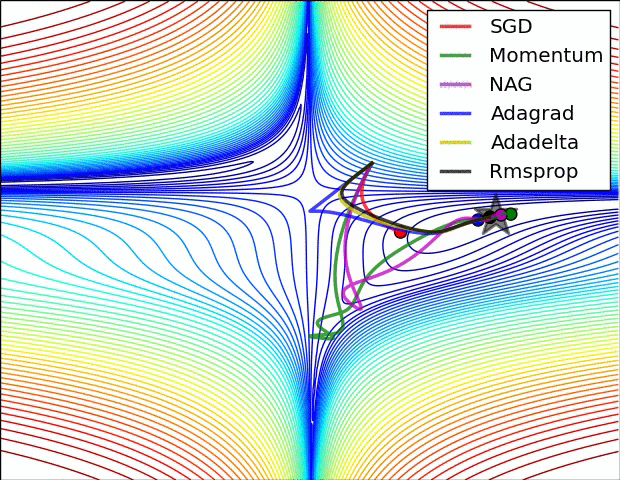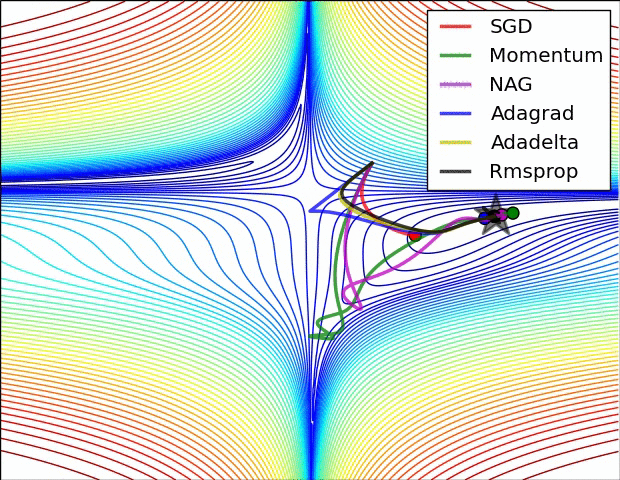
    "这是我们讲的最后一个优化算法，下面放一张各个优化算法的对比图结束这一节的内容\n",
    "\n",
    "![](https://raw.githubusercontent.com/cs231n/cs231n.github.io/master/assets/nn3/opt1.gif)\n",
    "\n",
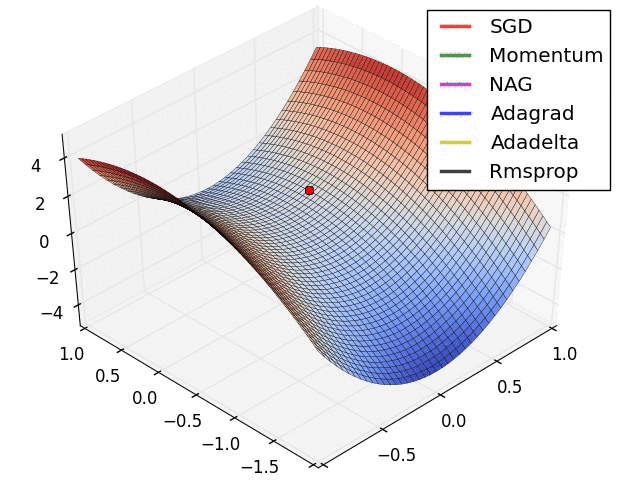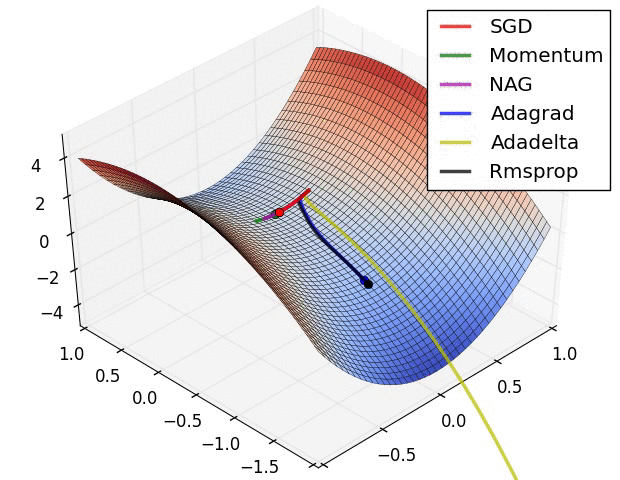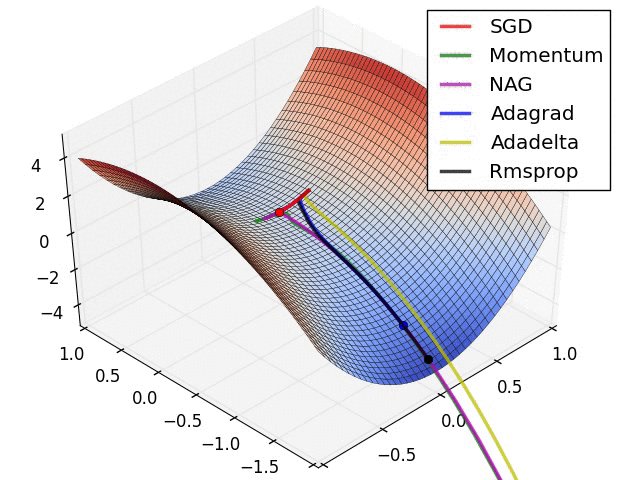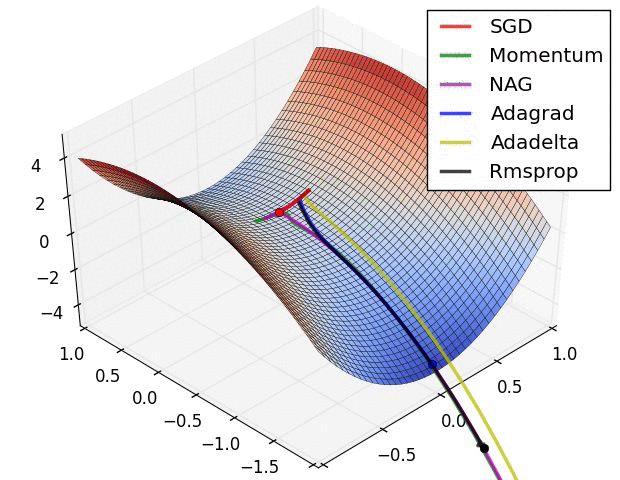    "![](https://raw.githubusercontent.com/cs231n/cs231n.github.io/master/assets/nn3/opt2.gif)\n",
    "\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "这两张图生动形象地展示了各种优化算法的实际效果"
   ]
  }
 ],
 "metadata": {
  "kernelspec": {
   "display_name": "Python 3",
   "language": "python",
   "name": "python3"
  },
  "language_info": {
   "codemirror_mode": {
    "name": "ipython",
    "version": 3
   },
   "file_extension": ".py",
   "mimetype": "text/x-python",
   "name": "python",
   "nbconvert_exporter": "python",
   "pygments_lexer": "ipython3",
   "version": "3.6.9"
  }
 },
 "nbformat": 4,
 "nbformat_minor": 2
}