OpenI
/
machinelearning_notebook
Not watched
1
0
Fork 0
Code
Releases 0 Wiki Activity
Issues 0 Pull Requests 0 Datasets Model Cloudbrain
Browse Source

Add order to some notebook

pull/1/MERGE
bushuhui 5 years ago
parent
58fb04b491
commit
5069f1d33c
37 changed files with 2345 additions and 3309 deletions
Split View
Diff Options
Show Stats Download Patch File Download Diff File
  1. +16
    -13
      5_nn/Perceptron.ipynb
  2. +2055
    -2035
      5_nn/mlp_bp.ipynb
  3. +2
    -1
      5_nn/softmax_ce.ipynb
  4. +7
    -15
      6_pytorch/0_basic/autograd.ipynb
  5. +0
    -0
      6_pytorch/1_NN/1-linear-regression-gradient-descend.ipynb
  6. +173
    -26
      6_pytorch/1_NN/2-logistic-regression.ipynb
  7. +0
    -0
      6_pytorch/1_NN/3-nn-sequential-module.ipynb
  8. +0
    -0
      6_pytorch/1_NN/4-deep-nn.ipynb
  9. +0
    -0
      6_pytorch/1_NN/5-param_initialize.ipynb
  10. +0
    -0
      6_pytorch/1_NN/6-nn_summary.ipynb
  11. +0
    -128
      6_pytorch/1_NN/bp.ipynb
  12. +0
    -0
      6_pytorch/1_NN/optimizer/6_1-sgd.ipynb
  13. +0
    -0
      6_pytorch/1_NN/optimizer/6_2-momentum.ipynb
  14. +0
    -0
      6_pytorch/1_NN/optimizer/6_3-adagrad.ipynb
  15. +0
    -0
      6_pytorch/1_NN/optimizer/6_4-rmsprop.ipynb
  16. +0
    -0
      6_pytorch/1_NN/optimizer/6_5-adadelta.ipynb
  17. +0
    -0
      6_pytorch/1_NN/optimizer/6_6-adam.ipynb
  18. +0
    -169
      6_pytorch/1_NN/optimizer/adadelta.py
  19. +0
    -182
      6_pytorch/1_NN/optimizer/adam.py
  20. +0
    -231
      6_pytorch/1_NN/optimizer/momentum.py
  21. +0
    -198
      6_pytorch/1_NN/optimizer/rmsprop.py
  22. +0
    -222
      6_pytorch/1_NN/optimizer/sgd.py
  23. +0
    -0
      6_pytorch/2_CNN/1-basic_conv.ipynb
  24. +0
    -0
      6_pytorch/2_CNN/2-batch-normalization.ipynb
  25. +0
    -0
      6_pytorch/2_CNN/3-lr-decay.ipynb
  26. +0
    -0
      6_pytorch/2_CNN/4-regularization.ipynb
  27. +0
    -0
      6_pytorch/2_CNN/5-data-augumentation.ipynb
  28. +0
    -0
      6_pytorch/2_CNN/6-vgg.ipynb
  29. +0
    -0
      6_pytorch/2_CNN/7-googlenet.ipynb
  30. +0
    -0
      6_pytorch/2_CNN/8-resnet.ipynb
  31. +0
    -0
      6_pytorch/2_CNN/9-densenet.ipynb
  32. BIN
      6_pytorch/2_CNN/CNN_Introduction.pptx
  33. +78
    -85
      6_pytorch/PyTorch_quick_intro.ipynb
  34. +3
    -0
      References.md
  35. +3
    -2
      demo_code/2_logistic_regression_1.py
  36. +3
    -1
      demo_code/2_logistic_regression_2.py
  37. +5
    -1
      requirements.txt

+ 16
- 13
5_nn/Perceptron.ipynb View File

@@ -59,7 +59,7 @@
"\n",
"假设训练数据集是线性可分的，感知机学习的目标是求得一个能够将训练数据的正负实例点完全分开的分离超平面，即最终求得参数w、b。这需要一个学习策略，即定义（经验）损失函数并将损失函数最小化。\n",
"\n",
"损失函数的一个自然的选择是误分类的点的总数。但是这样得到的损失函数不是参数w、b的连续可导函数，不宜优化。损失函数的另一个选择是误分类点到分里面的距离之和。\n",
"损失函数的一个自然的选择是误分类的点的总数。但是这样得到的损失函数不是参数w、b的连续可导函数，不宜优化。损失函数的另一个选择是误分类点到分类面的距离之和。\n",
"\n",
"首先，对于任意一点xo到超平面的距离为\n",
"$$\n",
@@ -124,10 +124,11 @@
"输出：w, b;感知机模型f(x)=sign(w·x+b)\n",
"(1) 初始化w0,b0\n",
"(2) 在训练数据集中选取（xi, yi）\n",
"(3) 如果yi(w xi+b)≤0\n",
"(3) 如果yi(w * xi+b)≤0\n",
" w = w + ηyixi\n",
" b = b + ηyi\n",
"(4) 转至（2）\n",
"(4) 如果所有的样本都正确分类，或者迭代次数超过设定值，则终止\n",
"(5) 否则，跳转至（2）\n",
"```\n",
"\n"
]
@@ -141,7 +142,7 @@
},
{
"cell_type": "code",
"execution_count": 1,
"execution_count": 3,
"metadata": {
"lines_to_end_of_cell_marker": 2
},
@@ -150,13 +151,15 @@
"name": "stdout",
"output_type": "stream",
"text": [
"update weight and bias: 1.0 3.0 0.5\n",
"update weight and bias: -0.5 2.5 0.0\n",
"update weight and bias: -2.5 2.0 -0.5\n",
"w = [-2.5, 2.0]\n",
"b = -0.5\n",
"[ 1 1 1 1 -1 -1 -1 -1]\n",
"[1, 1, 1, 1, -1, -1, -1, -1]\n"
"update weight and bias: 1.0 2.5 0.5\n",
"update weight and bias: -2.5 1.0 0.0\n",
"update weight and bias: -1.5 3.5 0.5\n",
"update weight and bias: -5.0 2.0 0.0\n",
"update weight and bias: -4.0 4.5 0.5\n",
"w = [-4.0, 4.5]\n",
"b = 0.5\n",
"ground_truth: [1, 1, 1, 1, -1, -1, -1, -1]\n",
"predicted: [1, 1, 1, 1, -1, -1, -1, -1]\n"
]
}
],
@@ -214,8 +217,8 @@
"# predict \n",
"y_pred = perceptron_pred(train_data, w, b)\n",
"\n",
"print(train_data[:, 2])\n",
"print(y_pred)"
"print(\"ground_truth: \", list(train_data[:, 2]))\n",
"print(\"predicted: \", y_pred)"
]
},
{


+ 2055
- 2035
5_nn/mlp_bp.ipynb
File diff suppressed because it is too large
View File


+ 2
- 1
5_nn/softmax_ce.ipynb View File

@@ -126,7 +126,8 @@
"\\frac{\\partial C}{\\partial z_i} & = & (-\\sum_j y_j \\frac{1}{a_j} ) \\frac{\\partial a_j}{\\partial z_i} \\\\\n",
" & = & - \\frac{y_i}{a_i} a_i ( 1 - a_i) + \\sum_{j \\ne i} \\frac{y_j}{a_j} a_i a_j \\\\\n",
" & = & -y_i + y_i a_i + \\sum_{j \\ne i} y_j a_i \\\\\n",
" & = & -y_i + a_i \\sum_{j} y_j\n",
" & = & -y_i + a_i \\sum_{j} y_j \\\\\n",
" & = & -y_i + a_i\n",
"\\end{eqnarray}"
]
},


+ 7
- 15
6_pytorch/0_basic/autograd.ipynb View File

@@ -10,10 +10,8 @@
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"import torch\n",
@@ -30,17 +28,14 @@
},
{
"cell_type": "code",
"execution_count": 2,
"execution_count": 3,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Variable containing:\n",
" 19\n",
"[torch.FloatTensor of size 1]\n",
"\n"
"tensor([19.], grad_fn=<AddBackward>)\n"
]
}
],
@@ -71,17 +66,14 @@
},
{
"cell_type": "code",
"execution_count": 3,
"execution_count": 4,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Variable containing:\n",
" 8\n",
"[torch.FloatTensor of size 1]\n",
"\n"
"tensor([8.])\n"
]
}
],
@@ -100,7 +92,7 @@
},
{
"cell_type": "code",
"execution_count": 4,
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [


6_pytorch/1_NN/linear-regression-gradient-descend.ipynb → 6_pytorch/1_NN/1-linear-regression-gradient-descend.ipynb View File


6_pytorch/1_NN/2-logistic-regression.ipynb
File diff suppressed because it is too large
View File


6_pytorch/1_NN/nn-sequential-module.ipynb → 6_pytorch/1_NN/3-nn-sequential-module.ipynb View File


6_pytorch/1_NN/deep-nn.ipynb → 6_pytorch/1_NN/4-deep-nn.ipynb View File


6_pytorch/1_NN/param_initialize.ipynb → 6_pytorch/1_NN/5-param_initialize.ipynb View File


6_pytorch/1_NN/nn_summary.ipynb → 6_pytorch/1_NN/6-nn_summary.ipynb View File


+ 0
- 128
6_pytorch/1_NN/bp.ipynb View File

@@ -1,128 +0,0 @@
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 反向传播算法\n",
"\n",
"前面我们介绍了三个模型，整个处理的基本流程都是定义模型，读入数据，给出损失函数$f$，通过梯度下降法更新参数。PyTorch 提供了非常简单的自动求导帮助我们求解导数，对于比较简单的模型，我们也能手动求出参数的梯度，但是对于非常复杂的模型，比如一个 100 层的网络，我们如何能够有效地手动求出这个梯度呢？这里就需要引入反向传播算法，自动求导本质是就是一个反向传播算法。\n",
"\n",
"反向传播算法是一个有效地求解梯度的算法，本质上其实就是一个链式求导法则的应用，然而这个如此简单而且显而易见的方法却是在 Roseblatt 提出感知机算法后将近 30 年才被发明和普及的，对此 Bengio 这样说道：“很多看似显而易见的想法只有在事后才变得的显而易见。”\n",
"\n",
"下面我们就来详细将一讲什么是反向传播算法。"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 链式法则\n",
"\n",
"首先来简单地介绍一下链式法则，考虑一个简单的函数，比如\n",
"$$f(x, y, z) = (x + y)z$$\n",
"\n",
"我们当然可以直接求出这个函数的微分，但是这里我们要使用链式法则，令\n",
"$$q=x+y$$\n",
"\n",
"那么\n",
"\n",
"$$f = qz$$\n",
"\n",
"对于这两个式子，我们可以分别求出他们的微分 \n",
"\n",
"$$\\frac{\\partial f}{\\partial q} = z, \\frac{\\partial f}{\\partial z}=q$$\n",
"\n",
"同时$q$是$x$和$y$的求和，所以我们能够得到\n",
"\n",
"$$\\frac{\\partial q}{x} = 1, \\frac{\\partial q}{y} = 1$$\n",
"\n",
"我们关心的问题是\n",
"\n",
"$$\\frac{\\partial f}{\\partial x}, \\frac{\\partial f}{\\partial y}, \\frac{\\partial f}{\\partial z}$$\n",
"\n",
"链式法则告诉我们如何来计算出他们的值\n",
"\n",
"$$\n",
"\\frac{\\partial f}{\\partial x} = \\frac{\\partial f}{\\partial q}\\frac{\\partial q}{\\partial x}\n",
"$$\n",
"$$\n",
"\\frac{\\partial f}{\\partial y} = \\frac{\\partial f}{\\partial q}\\frac{\\partial q}{\\partial y}\n",
"$$\n",
"$$\n",
"\\frac{\\partial f}{\\partial z} = q\n",
"$$\n",
"\n",
"通过链式法则我们知道如果我们需要对其中的元素求导，那么我们可以一层一层求导然后将结果乘起来，这就是链式法则的核心，也是反向传播算法的核心，更多关于链式法则的算法，可以访问这个[文档](https://zh.wikipedia.org/wiki/%E9%93%BE%E5%BC%8F%E6%B3%95%E5%88%99)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 反向传播算法\n",
"\n",
"了解了链式法则，我们就可以开始介绍反向传播算法了，本质上反向传播算法只是链式法则的一个应用。我们还是使用之前那个相同的例子$q=x+y, f=qz$，通过计算图可以将这个计算过程表达出来\n",
"\n",
"![](https://ws1.sinaimg.cn/large/006tNc79ly1fmiozcinyzj30c806vglk.jpg)\n",
"\n",
"上面绿色的数字表示其数值，下面红色的数字表示求出的梯度，我们可以一步一步看看反向传播算法的实现。首先从最后开始，梯度当然是1，然后计算\n",
"\n",
"$$\\frac{\\partial f}{\\partial q} = z = -4,\\ \\frac{\\partial f}{\\partial z} = q = 3$$\n",
"\n",
"接着我们计算\n",
"$$\\frac{\\partial f}{\\partial x} = \\frac{\\partial f}{\\partial q} \\frac{\\partial q}{\\partial x} = -4 \\times 1 = -4,\\ \\frac{\\partial f}{\\partial y} = \\frac{\\partial f}{\\partial q} \\frac{\\partial q}{\\partial y} = -4 \\times 1 = -4$$\n",
"\n",
"这样一步一步我们就求出了$\\nabla f(x, y, z)$。\n",
"\n",
"直观上看反向传播算法是一个优雅的局部过程，每次求导只是对当前的运算求导，求解每层网络的参数都是通过链式法则将前面的结果求出不断迭代到这一层，所以说这是一个传播过程\n",
"\n",
"### Sigmoid函数举例\n",
"\n",
"下面我们通过Sigmoid函数来演示反向传播过程在一个复杂的函数上是如何进行的。\n",
"\n",
"$$\n",
"f(w, x) = \\frac{1}{1+e^{-(w_0 x_0 + w_1 x_1 + w_2)}}\n",
"$$\n",
"\n",
"我们需要求解出\n",
"$$\\frac{\\partial f}{\\partial w_0}, \\frac{\\partial f}{\\partial w_1}, \\frac{\\partial f}{\\partial w_2}$$\n",
"\n",
"首先我们将这个函数抽象成一个计算图来表示，即\n",
"$$\n",
" f(x) = \\frac{1}{x} \\\\\n",
" f_c(x) = 1 + x \\\\\n",
" f_e(x) = e^x \\\\\n",
" f_w(x) = -(w_0 x_0 + w_1 x_1 + w_2)\n",
"$$\n",
"\n",
"这样我们就能够画出下面的计算图\n",
"\n",
"![](https://ws1.sinaimg.cn/large/006tNc79ly1fmip1va5qjj30lb08e0t0.jpg)\n",
"\n",
"同样上面绿色的数子表示数值，下面红色的数字表示梯度，我们从后往前计算一下各个参数的梯度。首先最后面的梯度是1,，然后经过$\\frac{1}{x}$这个函数，这个函数的梯度是$-\\frac{1}{x^2}$，所以往前传播的梯度是$1 \\times -\\frac{1}{1.37^2} = -0.53$，然后是$+1$这个操作，梯度不变，接着是$e^x$这个运算，它的梯度就是$-0.53 \\times e^{-1} = -0.2$，这样不断往后传播就能够求得每个参数的梯度。"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 2
}

6_pytorch/1_NN/optimizer/sgd.ipynb → 6_pytorch/1_NN/optimizer/6_1-sgd.ipynb View File


6_pytorch/1_NN/optimizer/momentum.ipynb → 6_pytorch/1_NN/optimizer/6_2-momentum.ipynb View File


6_pytorch/1_NN/optimizer/adagrad.ipynb → 6_pytorch/1_NN/optimizer/6_3-adagrad.ipynb View File


6_pytorch/1_NN/optimizer/rmsprop.ipynb → 6_pytorch/1_NN/optimizer/6_4-rmsprop.ipynb View File


6_pytorch/1_NN/optimizer/adadelta.ipynb → 6_pytorch/1_NN/optimizer/6_5-adadelta.ipynb View File


6_pytorch/1_NN/optimizer/adam.ipynb → 6_pytorch/1_NN/optimizer/6_6-adam.ipynb View File


+ 0
- 169
6_pytorch/1_NN/optimizer/adadelta.py View File

@@ -1,169 +0,0 @@
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext_format_version: '1.2'
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# language_info:
# codemirror_mode:
# name: ipython
# version: 3
# file_extension: .py
# mimetype: text/x-python
# name: python
# nbconvert_exporter: python
# pygments_lexer: ipython3
# version: 3.5.2
# ---

# # Adadelta
# Adadelta 算是 Adagrad 法的延伸，它跟 RMSProp 一样，都是为了解决 Adagrad 中学习率不断减小的问题，RMSProp 是通过移动加权平均的方式，而 Adadelta 也是一种方法，有趣的是，它并不需要学习率这个参数。
#
# ## Adadelta 法
# Adadelta 跟 RMSProp 一样，先使用移动平均来计算 s
#
# $$
# s = \rho s + (1 - \rho) g^2
# $$
#
# 这里 $\rho$ 和 RMSProp 中的 $\alpha$ 都是移动平均系数，g 是参数的梯度，然后我们会计算需要更新的参数的变化量
#
# $$
# g' = \frac{\sqrt{\Delta \theta + \epsilon}}{\sqrt{s + \epsilon}} g
# $$
#
# $\Delta \theta$ 初始为 0 张量，每一步做如下的指数加权移动平均更新
#
# $$
# \Delta \theta = \rho \Delta \theta + (1 - \rho) g'^2
# $$
#
# 最后参数更新如下
#
# $$
# \theta = \theta - g'
# $$
#
# 下面我们实现以下 Adadelta

def adadelta(parameters, sqrs, deltas, rho):
eps = 1e-6
for param, sqr, delta in zip(parameters, sqrs, deltas):
sqr[:] = rho * sqr + (1 - rho) * param.grad.data ** 2
cur_delta = torch.sqrt(delta + eps) / torch.sqrt(sqr + eps) * param.grad.data
delta[:] = rho * delta + (1 - rho) * cur_delta ** 2
param.data = param.data - cur_delta

# +
import numpy as np
import torch
from torchvision.datasets import MNIST # 导入 pytorch 内置的 mnist 数据
from torch.utils.data import DataLoader
from torch import nn
from torch.autograd import Variable
import time
import matplotlib.pyplot as plt
# %matplotlib inline

def data_tf(x):
x = np.array(x, dtype='float32') / 255
x = (x - 0.5) / 0.5 # 标准化，这个技巧之后会讲到
x = x.reshape((-1,)) # 拉平
x = torch.from_numpy(x)
return x

train_set = MNIST('./data', train=True, transform=data_tf, download=True) # 载入数据集，申明定义的数据变换
test_set = MNIST('./data', train=False, transform=data_tf, download=True)

# 定义 loss 函数
criterion = nn.CrossEntropyLoss()

# +
train_data = DataLoader(train_set, batch_size=64, shuffle=True)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)

# 初始化梯度平方项和 delta 项
sqrs = []
deltas = []
for param in net.parameters():
sqrs.append(torch.zeros_like(param.data))
deltas.append(torch.zeros_like(param.data))

# 开始训练
losses = []
idx = 0
start = time.time() # 记时开始
for e in range(5):
train_loss = 0
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# 前向传播
out = net(im)
loss = criterion(out, label)
# 反向传播
net.zero_grad()
loss.backward()
adadelta(net.parameters(), sqrs, deltas, 0.9) # rho 设置为 0.9
# 记录误差
train_loss += loss.data[0]
if idx % 30 == 0:
losses.append(loss.data[0])
idx += 1
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))
# -

x_axis = np.linspace(0, 5, len(losses), endpoint=True)
plt.semilogy(x_axis, losses, label='rho=0.99')
plt.legend(loc='best')

# 可以看到使用 adadelta 跑 5 次能够得到更小的 loss

# **小练习：思考一下为什么 Adadelta 没有学习率这个参数，它是被什么代替了**

# 当然 pytorch 也内置了 adadelta 的方法，非常简单，只需要调用 `torch.optim.Adadelta()` 就可以了，下面是例子

# +
train_data = DataLoader(train_set, batch_size=64, shuffle=True)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)

optimizer = torch.optim.Adadelta(net.parameters(), rho=0.9)

# 开始训练
start = time.time() # 记时开始
for e in range(5):
train_loss = 0
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# 前向传播
out = net(im)
loss = criterion(out, label)
# 反向传播
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 记录误差
train_loss += loss.data[0]
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))
# -

# **小练习：看看 pytorch 中的 adadelta，里面是有学习率这个参数，但是前面我们讲过 adadelta 不用设置学习率，看看这个学习率到底是干嘛的**

+ 0
- 182
6_pytorch/1_NN/optimizer/adam.py View File

@@ -1,182 +0,0 @@
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext_format_version: '1.2'
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# language_info:
# codemirror_mode:
# name: ipython
# version: 3
# file_extension: .py
# mimetype: text/x-python
# name: python
# nbconvert_exporter: python
# pygments_lexer: ipython3
# version: 3.5.2
# ---

# # Adam
# Adam 是一个结合了动量法和 RMSProp 的优化算法，其结合了两者的优点。
#
# ## Adam 算法
# Adam 算法会使用一个动量变量 v 和一个 RMSProp 中的梯度元素平方的移动指数加权平均 s，首先将他们全部初始化为 0，然后在每次迭代中，计算他们的移动加权平均进行更新
#
# $$
# v = \beta_1 v + (1 - \beta_1) g \\
# s = \beta_2 s + (1 - \beta_2) g^2
# $$
#
# 在 adam 算法里，为了减轻 v 和 s 被初始化为 0 的初期对计算指数加权移动平均的影响，每次 v 和 s 都做下面的修正
#
# $$
# \hat{v} = \frac{v}{1 - \beta_1^t} \\
# \hat{s} = \frac{s}{1 - \beta_2^t}
# $$
#
# 这里 t 是迭代次数，可以看到，当 $0 \leq \beta_1, \beta_2 \leq 1$ 的时候，迭代到后期 t 比较大，那么 $\beta_1^t$ 和 $\beta_2^t$ 就几乎为 0，就不会对 v 和 s 有任何影响了，算法作者建议$\beta_1 = 0.9$, $\beta_2 = 0.999$。
#
# 最后使用修正之后的 $\hat{v}$ 和 $\hat{s}$ 进行学习率的重新计算
#
# $$
# g' = \frac{\eta \hat{v}}{\sqrt{\hat{s} + \epsilon}}
# $$
#
# 这里 $\eta$ 是学习率，$epsilon$ 仍然是为了数值稳定性而添加的常数，最后参数更新有
#
# $$
# \theta_i = \theta_{i-1} - g'
# $$

# 下面我们来实现以下 adam 算法

def adam(parameters, vs, sqrs, lr, t, beta1=0.9, beta2=0.999):
eps = 1e-8
for param, v, sqr in zip(parameters, vs, sqrs):
v[:] = beta1 * v + (1 - beta1) * param.grad.data
sqr[:] = beta2 * sqr + (1 - beta2) * param.grad.data ** 2
v_hat = v / (1 - beta1 ** t)
s_hat = sqr / (1 - beta2 ** t)
param.data = param.data - lr * v_hat / torch.sqrt(s_hat + eps)

# +
import numpy as np
import torch
from torchvision.datasets import MNIST # 导入 pytorch 内置的 mnist 数据
from torch.utils.data import DataLoader
from torch import nn
from torch.autograd import Variable
import time
import matplotlib.pyplot as plt
# %matplotlib inline

def data_tf(x):
x = np.array(x, dtype='float32') / 255
x = (x - 0.5) / 0.5 # 标准化，这个技巧之后会讲到
x = x.reshape((-1,)) # 拉平
x = torch.from_numpy(x)
return x

train_set = MNIST('../../../data/mnist', train=True, transform=data_tf, download=True) # 载入数据集，申明定义的数据变换
test_set = MNIST('../../../data/mnist', train=False, transform=data_tf, download=True)

# 定义 loss 函数
criterion = nn.CrossEntropyLoss()

# +
train_data = DataLoader(train_set, batch_size=64, shuffle=True)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)

# 初始化梯度平方项和动量项
sqrs = []
vs = []
for param in net.parameters():
sqrs.append(torch.zeros_like(param.data))
vs.append(torch.zeros_like(param.data))
t = 1
# 开始训练
losses = []
idx = 0

start = time.time() # 记时开始
for e in range(5):
train_loss = 0
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# 前向传播
out = net(im)
loss = criterion(out, label)
# 反向传播
net.zero_grad()
loss.backward()
adam(net.parameters(), vs, sqrs, 1e-3, t) # 学习率设为 0.001
t += 1
# 记录误差
train_loss += loss.data[0]
if idx % 30 == 0:
losses.append(loss.data[0])
idx += 1
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))
# -

x_axis = np.linspace(0, 5, len(losses), endpoint=True)
plt.semilogy(x_axis, losses, label='adam')
plt.legend(loc='best')

# 可以看到使用 adam 算法 loss 能够更快更好地收敛，但是一定要小心学习率的设定，使用自适应的算法一般需要更小的学习率
#
# 当然 pytorch 中也内置了 adam 的实现，只需要调用 `torch.optim.Adam()`，下面是例子

# +
train_data = DataLoader(train_set, batch_size=64, shuffle=True)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)

optimizer = torch.optim.Adam(net.parameters(), lr=1e-3)
# 开始训练
start = time.time() # 记时开始
for e in range(5):
train_loss = 0
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# 前向传播
out = net(im)
loss = criterion(out, label)
# 反向传播
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 记录误差
train_loss += loss.data[0]
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))
# -

# 这是我们讲的最后一个优化算法，下面放一张各个优化算法的对比图结束这一节的内容
#
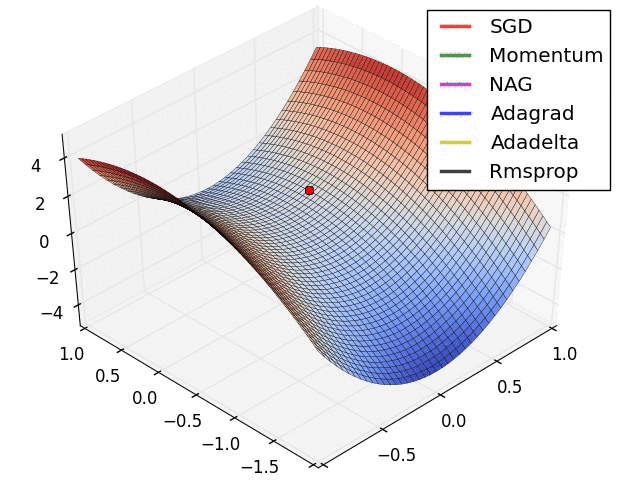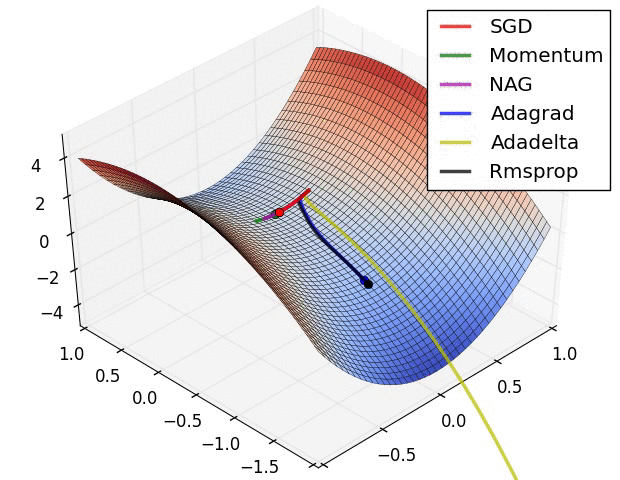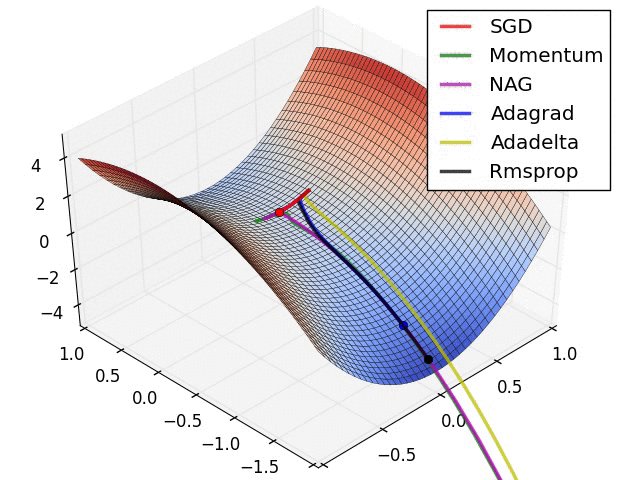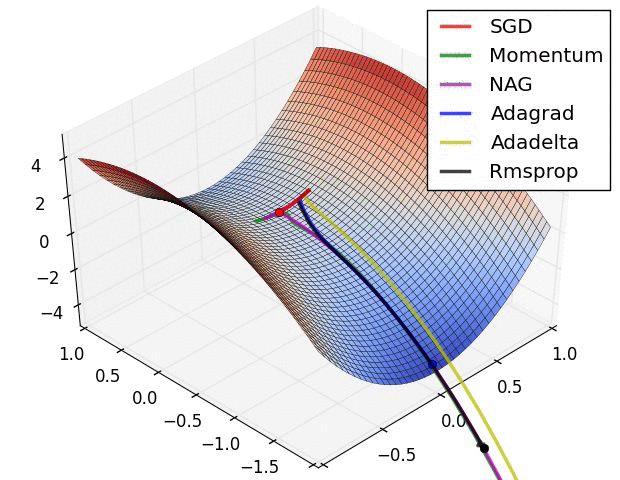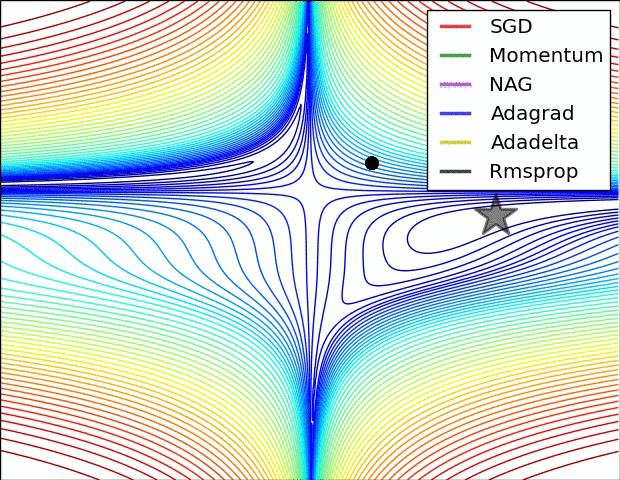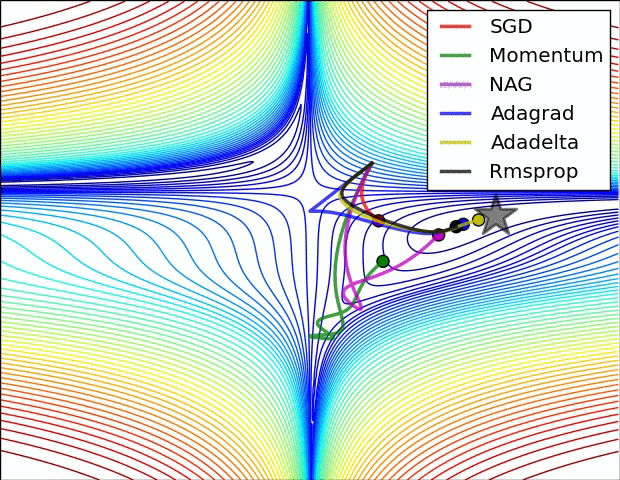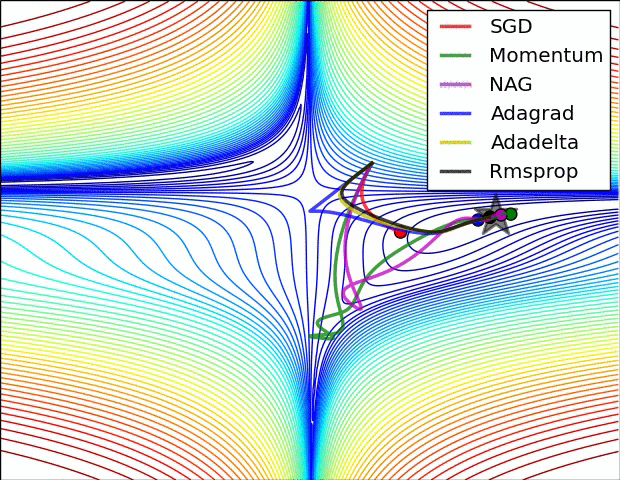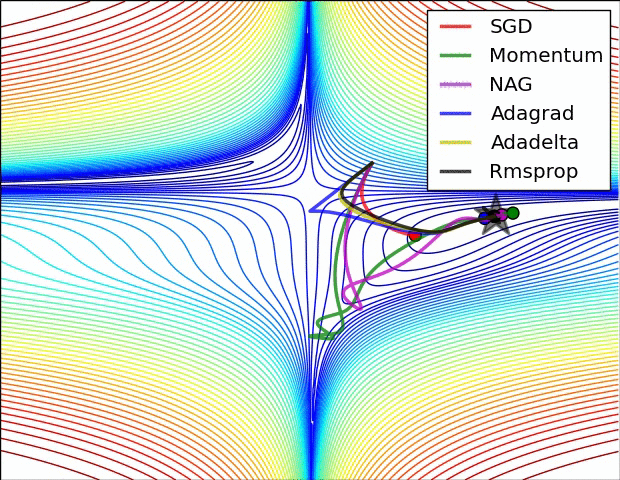# ![](https://raw.githubusercontent.com/cs231n/cs231n.github.io/master/assets/nn3/opt1.gif)
#
# ![](https://raw.githubusercontent.com/cs231n/cs231n.github.io/master/assets/nn3/opt2.gif)
#
#

# 这两张图生动形象地展示了各种优化算法的实际效果

+ 0
- 231
6_pytorch/1_NN/optimizer/momentum.py View File

@@ -1,231 +0,0 @@
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext_format_version: '1.2'
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# language_info:
# codemirror_mode:
# name: ipython
# version: 3
# file_extension: .py
# mimetype: text/x-python
# name: python
# nbconvert_exporter: python
# pygments_lexer: ipython3
# version: 3.5.2
# ---

# # 动量法
# 使用梯度下降法，每次都会朝着目标函数下降最快的方向，这也称为最速下降法。这种更新方法看似非常快，实际上存在一些问题。
#
# ## 梯度下降法的问题
# 考虑一个二维输入，$[x_1, x_2]$，输出的损失函数 $L: R^2 \rightarrow R$，下面是这个函数的等高线
#
# ![](https://ws1.sinaimg.cn/large/006tKfTcly1fmnketw5f4j30az04lq31.jpg)
#
# 可以想象成一个很扁的漏斗，这样在竖直方向上，梯度就非常大，在水平方向上，梯度就相对较小，所以我们在设置学习率的时候就不能设置太大，为了防止竖直方向上参数更新太过了，这样一个较小的学习率又导致了水平方向上参数在更新的时候太过于缓慢，所以就导致最终收敛起来非常慢。
#
# ## 动量法
# 动量法的提出就是为了应对这个问题，我们梯度下降法做一个修改如下
#
# $$
# v_i = \gamma v_{i-1} + \eta \nabla L(\theta)
# $$
# $$
# \theta_i = \theta_{i-1} - v_i
# $$
#
# 其中 $v_i$ 是当前速度，$\gamma$ 是动量参数，是一个小于 1的正数，$\eta$ 是学习率

# 相当于每次在进行参数更新的时候，都会将之前的速度考虑进来，每个参数在各方向上的移动幅度不仅取决于当前的梯度，还取决于过去各个梯度在各个方向上是否一致，如果一个梯度一直沿着当前方向进行更新，那么每次更新的幅度就越来越大，如果一个梯度在一个方向上不断变化，那么其更新幅度就会被衰减，这样我们就可以使用一个较大的学习率，使得收敛更快，同时梯度比较大的方向就会因为动量的关系每次更新的幅度减少，如下图
#
# ![](https://ws1.sinaimg.cn/large/006tNc79gy1fmo5l53o76j30ak04gjrh.jpg)
#
# 比如我们的梯度每次都等于 g，而且方向都相同，那么动量法在该方向上使参数加速移动，有下面的公式：
#
# $$
# v_0 = 0
# $$
# $$
# v_1 = \gamma v_0 + \eta g = \eta g
# $$
# $$
# v_2 = \gamma v_1 + \eta g = (1 + \gamma) \eta g
# $$
# $$
# v_3 = \gamma v_2 + \eta g = (1 + \gamma + \gamma^2) \eta g
# $$
# $$
# \cdots
# $$
# $$
# v_{+ \infty} = (1 + \gamma + \gamma^2 + \gamma^3 + \cdots) \eta g = \frac{1}{1 - \gamma} \eta g
# $$
#
# 如果我们把 $\gamma$ 定为 0.9，那么更新幅度的峰值就是原本梯度乘学习率的 10 倍。
#
# 本质上说，动量法就仿佛我们从高坡上推一个球，小球在向下滚动的过程中积累了动量，在途中也会变得越来越快，最后会达到一个峰值，对应于我们的算法中就是，动量项会沿着梯度指向方向相同的方向不断增大，对于梯度方向改变的方向逐渐减小，得到了更快的收敛速度以及更小的震荡。
#
# 下面我们手动实现一个动量法，公式已经在上面了

def sgd_momentum(parameters, vs, lr, gamma):
for param, v in zip(parameters, vs):
v[:] = gamma * v + lr * param.grad.data
param.data = param.data - v

# +
import numpy as np
import torch
from torchvision.datasets import MNIST # 导入 pytorch 内置的 mnist 数据
from torch.utils.data import DataLoader
from torch import nn
from torch.autograd import Variable
import time
import matplotlib.pyplot as plt
# %matplotlib inline

def data_tf(x):
x = np.array(x, dtype='float32') / 255
x = (x - 0.5) / 0.5 # 标准化，这个技巧之后会讲到
x = x.reshape((-1,)) # 拉平
x = torch.from_numpy(x)
return x

train_set = MNIST('./data', train=True, transform=data_tf, download=True) # 载入数据集，申明定义的数据变换
test_set = MNIST('./data', train=False, transform=data_tf, download=True)

# 定义 loss 函数
criterion = nn.CrossEntropyLoss()

# +
train_data = DataLoader(train_set, batch_size=64, shuffle=True)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)

# 将速度初始化为和参数形状相同的零张量
vs = []
for param in net.parameters():
vs.append(torch.zeros_like(param.data))
# 开始训练
losses = []

start = time.time() # 记时开始
for e in range(5):
train_loss = 0
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# 前向传播
out = net(im)
loss = criterion(out, label)
# 反向传播
net.zero_grad()
loss.backward()
sgd_momentum(net.parameters(), vs, 1e-2, 0.9) # 使用的动量参数为 0.9，学习率 0.01
# 记录误差
train_loss += loss.data[0]
losses.append(loss.data[0])
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))
# -

# 可以看到，加完动量之后 loss 能下降非常快，但是一定要小心学习率和动量参数，这两个值会直接影响到参数每次更新的幅度，所以可以多试几个值

# 当然，pytorch 内置了动量法的实现，非常简单，直接在 `torch.optim.SGD(momentum=0.9)` 即可，下面实现一下

# +
train_data = DataLoader(train_set, batch_size=64, shuffle=True)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)

optimizer = torch.optim.SGD(net.parameters(), lr=1e-2, momentum=0.9) # 加动量
# 开始训练
losses = []
idx = 0
start = time.time() # 记时开始
for e in range(5):
train_loss = 0
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# 前向传播
out = net(im)
loss = criterion(out, label)
# 反向传播
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 记录误差
train_loss += loss.data[0]
if idx % 30 == 0: # 30 步记录一次
losses.append(loss.data[0])
idx += 1
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))
# -

x_axis = np.linspace(0, 5, len(losses), endpoint=True)
plt.semilogy(x_axis, losses, label='momentum: 0.9')
plt.legend(loc='best')

# 我们可以对比一下不加动量的随机梯度下降法

# +
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)

optimizer = torch.optim.SGD(net.parameters(), lr=1e-2) # 不加动量
# 开始训练
losses1 = []
idx = 0
start = time.time() # 记时开始
for e in range(5):
train_loss = 0
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# 前向传播
out = net(im)
loss = criterion(out, label)
# 反向传播
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 记录误差
train_loss += loss.data[0]
if idx % 30 == 0: # 30 步记录一次
losses1.append(loss.data[0])
idx += 1
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))
# -

x_axis = np.linspace(0, 5, len(losses), endpoint=True)
plt.semilogy(x_axis, losses, label='momentum: 0.9')
plt.semilogy(x_axis, losses1, label='no momentum')
plt.legend(loc='best')

# 可以看到加完动量之后的 loss 下降的程度更低了，可以将动量理解为一种惯性作用，所以每次更新的幅度都会比不加动量的情况更多

+ 0
- 198
6_pytorch/1_NN/optimizer/rmsprop.py View File

@@ -1,198 +0,0 @@
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext_format_version: '1.2'
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# language_info:
# codemirror_mode:
# name: ipython
# version: 3
# file_extension: .py
# mimetype: text/x-python
# name: python
# nbconvert_exporter: python
# pygments_lexer: ipython3
# version: 3.5.2
# ---

# # RMSProp
# RMSprop 是由 Geoff Hinton 在他 Coursera 课程中提出的一种适应性学习率方法，至今仍未被公开发表。前面我们提到了 Adagrad 算法有一个问题，就是学习率分母上的变量 s 不断被累加增大，最后会导致学习率除以一个比较大的数之后变得非常小，这不利于我们找到最后的最优解，所以 RMSProp 的提出就是为了解决这个问题。
#
# ## RMSProp 算法
# RMSProp 仍然会使用梯度的平方量，不同于 Adagrad，其会使用一个指数加权移动平均来计算这个 s，也就是
#
# $$
# s_i = \alpha s_{i-1} + (1 - \alpha) \ g^2
# $$
#
# 这里 g 表示当前求出的参数梯度，然后最终更新和 Adagrad 是一样的，学习率变成了
#
# $$
# \frac{\eta}{\sqrt{s + \epsilon}}
# $$
#
# 这里 $\alpha$ 是一个移动平均的系数，也是因为这个系数，导致了 RMSProp 和 Adagrad 不同的地方，这个系数使得 RMSProp 更新到后期累加的梯度平方较小，从而保证 s 不会太大，也就使得模型后期依然能够找到比较优的结果
#
# 实现上和 Adagrad 非常像

def rmsprop(parameters, sqrs, lr, alpha):
eps = 1e-10
for param, sqr in zip(parameters, sqrs):
sqr[:] = alpha * sqr + (1 - alpha) * param.grad.data ** 2
div = lr / torch.sqrt(sqr + eps) * param.grad.data
param.data = param.data - div

# +
import numpy as np
import torch
from torchvision.datasets import MNIST # 导入 pytorch 内置的 mnist 数据
from torch.utils.data import DataLoader
from torch import nn
from torch.autograd import Variable
import time
import matplotlib.pyplot as plt
# %matplotlib inline

def data_tf(x):
x = np.array(x, dtype='float32') / 255
x = (x - 0.5) / 0.5 # 标准化，这个技巧之后会讲到
x = x.reshape((-1,)) # 拉平
x = torch.from_numpy(x)
return x

train_set = MNIST('./data', train=True, transform=data_tf, download=True) # 载入数据集，申明定义的数据变换
test_set = MNIST('./data', train=False, transform=data_tf, download=True)

# 定义 loss 函数
criterion = nn.CrossEntropyLoss()

# +
train_data = DataLoader(train_set, batch_size=64, shuffle=True)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)

# 初始化梯度平方项
sqrs = []
for param in net.parameters():
sqrs.append(torch.zeros_like(param.data))
# 开始训练
losses = []
idx = 0
start = time.time() # 记时开始
for e in range(5):
train_loss = 0
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# 前向传播
out = net(im)
loss = criterion(out, label)
# 反向传播
net.zero_grad()
loss.backward()
rmsprop(net.parameters(), sqrs, 1e-3, 0.9) # 学习率设为 0.001，alpha 设为 0.9
# 记录误差
train_loss += loss.data[0]
if idx % 30 == 0:
losses.append(loss.data[0])
idx += 1
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))
# -

x_axis = np.linspace(0, 5, len(losses), endpoint=True)
plt.semilogy(x_axis, losses, label='alpha=0.9')
plt.legend(loc='best')

# +
train_data = DataLoader(train_set, batch_size=64, shuffle=True)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)

# 初始化梯度平方项
sqrs = []
for param in net.parameters():
sqrs.append(torch.zeros_like(param.data))
# 开始训练
losses = []
idx = 0

start = time.time() # 记时开始
for e in range(5):
train_loss = 0
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# 前向传播
out = net(im)
loss = criterion(out, label)
# 反向传播
net.zero_grad()
loss.backward()
rmsprop(net.parameters(), sqrs, 1e-3, 0.999) # 学习率设为 0.001，alpha 设为 0.999
# 记录误差
train_loss += loss.data[0]
if idx % 30 == 0:
losses.append(loss.data[0])
idx += 1
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))
# -

x_axis = np.linspace(0, 5, len(losses), endpoint=True)
plt.semilogy(x_axis, losses, label='alpha=0.999')
plt.legend(loc='best')

# **小练习：可以看到使用了不同的 alpha 会使得 loss 在下降过程中的震荡程度不同，想想为什么**

# 当然 pytorch 也内置了 rmsprop 的方法，非常简单，只需要调用 `torch.optim.RMSprop()` 就可以了，下面是例子

# +
train_data = DataLoader(train_set, batch_size=64, shuffle=True)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)

optimizer = torch.optim.RMSprop(net.parameters(), lr=1e-3, alpha=0.9)
# 开始训练

start = time.time() # 记时开始
for e in range(5):
train_loss = 0
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# 前向传播
out = net(im)
loss = criterion(out, label)
# 反向传播
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 记录误差
train_loss += loss.data[0]
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))

+ 0
- 222
6_pytorch/1_NN/optimizer/sgd.py View File

@@ -1,222 +0,0 @@
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext_format_version: '1.2'
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# language_info:
# codemirror_mode:
# name: ipython
# version: 3
# file_extension: .py
# mimetype: text/x-python
# name: python
# nbconvert_exporter: python
# pygments_lexer: ipython3
# version: 3.5.2
# ---

# # 随机梯度下降法
# 前面我们介绍了梯度下降法的数学原理，下面我们通过例子来说明一下随机梯度下降法，我们分别从 0 自己实现，以及使用 pytorch 中自带的优化器

# +
import numpy as np
import torch
from torchvision.datasets import MNIST # 导入 pytorch 内置的 mnist 数据
from torch.utils.data import DataLoader
from torch import nn
from torch.autograd import Variable
import time
import matplotlib.pyplot as plt
# %matplotlib inline

def data_tf(x):
x = np.array(x, dtype='float32') / 255 # 将数据变到 0 ~ 1 之间
x = (x - 0.5) / 0.5 # 标准化，这个技巧之后会讲到
x = x.reshape((-1,)) # 拉平
x = torch.from_numpy(x)
return x

train_set = MNIST('./data', train=True, transform=data_tf, download=True) # 载入数据集，申明定义的数据变换
test_set = MNIST('./data', train=False, transform=data_tf, download=True)

# 定义 loss 函数
criterion = nn.CrossEntropyLoss()
# -

# 随机梯度下降法非常简单，公式就是
# $$
# \theta_{i+1} = \theta_i - \eta \nabla L(\theta)
# $$
# 非常简单，我们可以从 0 开始自己实现

def sgd_update(parameters, lr):
for param in parameters:
param.data = param.data - lr * param.grad.data

# 我们可以将 batch size 先设置为 1，看看有什么效果

# +
train_data = DataLoader(train_set, batch_size=1, shuffle=True)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)

# 开始训练
losses1 = []
idx = 0

start = time.time() # 记时开始
for e in range(5):
train_loss = 0
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# 前向传播
out = net(im)
loss = criterion(out, label)
# 反向传播
net.zero_grad()
loss.backward()
sgd_update(net.parameters(), 1e-2) # 使用 0.01 的学习率
# 记录误差
train_loss += loss.data[0]
if idx % 30 == 0:
losses1.append(loss.data[0])
idx += 1
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))
# -

x_axis = np.linspace(0, 5, len(losses1), endpoint=True)
plt.semilogy(x_axis, losses1, label='batch_size=1')
plt.legend(loc='best')

# 可以看到，loss 在剧烈震荡，因为每次都是只对一个样本点做计算，每一层的梯度都具有很高的随机性，而且需要耗费了大量的时间

# +
train_data = DataLoader(train_set, batch_size=64, shuffle=True)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)

# 开始训练
losses2 = []
idx = 0
start = time.time() # 记时开始
for e in range(5):
train_loss = 0
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# 前向传播
out = net(im)
loss = criterion(out, label)
# 反向传播
net.zero_grad()
loss.backward()
sgd_update(net.parameters(), 1e-2)
# 记录误差
train_loss += loss.data[0]
if idx % 30 == 0:
losses2.append(loss.data[0])
idx += 1
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))
# -

x_axis = np.linspace(0, 5, len(losses2), endpoint=True)
plt.semilogy(x_axis, losses2, label='batch_size=64')
plt.legend(loc='best')

# 通过上面的结果可以看到 loss 没有 batch 等于 1 震荡那么距离，同时也可以降到一定的程度了，时间上也比之前快了非常多，因为按照 batch 的数据量计算上更快，同时梯度对比于 batch size = 1 的情况也跟接近真实的梯度，所以 batch size 的值越大，梯度也就越稳定，而 batch size 越小，梯度具有越高的随机性，这里 batch size 为 64，可以看到 loss 仍然存在震荡，但这并没有关系，如果 batch size 太大，对于内存的需求就更高，同时也不利于网络跳出局部极小点，所以现在普遍使用基于 batch 的随机梯度下降法，而 batch 的多少基于实际情况进行考虑

# 下面我们调高学习率，看看有什么样的结果

# +
train_data = DataLoader(train_set, batch_size=64, shuffle=True)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)

# 开始训练
losses3 = []
idx = 0
start = time.time() # 记时开始
for e in range(5):
train_loss = 0
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# 前向传播
out = net(im)
loss = criterion(out, label)
# 反向传播
net.zero_grad()
loss.backward()
sgd_update(net.parameters(), 1) # 使用 1.0 的学习率
# 记录误差
train_loss += loss.data[0]
if idx % 30 == 0:
losses3.append(loss.data[0])
idx += 1
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))
# -

x_axis = np.linspace(0, 5, len(losses3), endpoint=True)
plt.semilogy(x_axis, losses3, label='lr = 1')
plt.legend(loc='best')

# 可以看到，学习率太大会使得损失函数不断回跳，从而无法让损失函数较好降低，所以我们一般都是用一个比较小的学习率

# 实际上我们并不用自己造轮子，因为 pytorch 中已经为我们内置了随机梯度下降发，而且之前我们一直在使用，下面我们来使用 pytorch 自带的优化器来实现随机梯度下降

# +
train_data = DataLoader(train_set, batch_size=64, shuffle=True)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)

optimzier = torch.optim.SGD(net.parameters(), 1e-2)
# 开始训练

start = time.time() # 记时开始
for e in range(5):
train_loss = 0
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# 前向传播
out = net(im)
loss = criterion(out, label)
# 反向传播
optimzier.zero_grad()
loss.backward()
optimzier.step()
# 记录误差
train_loss += loss.data[0]
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))

6_pytorch/2_CNN/basic_conv.ipynb → 6_pytorch/2_CNN/1-basic_conv.ipynb View File


6_pytorch/2_CNN/batch-normalization.ipynb → 6_pytorch/2_CNN/2-batch-normalization.ipynb View File


6_pytorch/2_CNN/lr-decay.ipynb → 6_pytorch/2_CNN/3-lr-decay.ipynb View File


6_pytorch/2_CNN/regularization.ipynb → 6_pytorch/2_CNN/4-regularization.ipynb View File


6_pytorch/2_CNN/data-augumentation.ipynb → 6_pytorch/2_CNN/5-data-augumentation.ipynb View File


6_pytorch/2_CNN/vgg.ipynb → 6_pytorch/2_CNN/6-vgg.ipynb View File


6_pytorch/2_CNN/googlenet.ipynb → 6_pytorch/2_CNN/7-googlenet.ipynb View File


6_pytorch/2_CNN/resnet.ipynb → 6_pytorch/2_CNN/8-resnet.ipynb View File


6_pytorch/2_CNN/densenet.ipynb → 6_pytorch/2_CNN/9-densenet.ipynb View File


BIN
6_pytorch/2_CNN/CNN_Introduction.pptx View File


+ 78
- 85
6_pytorch/PyTorch_quick_intro.ipynb View File

@@ -41,11 +41,11 @@
{
"data": {
"text/plain": [
"tensor([[3.7158e-37, 0.0000e+00, 5.7453e-44],\n",
" [0.0000e+00, nan, 4.5745e-41],\n",
" [1.3733e-14, 6.4076e+07, 2.0706e-19],\n",
" [7.3909e+22, 2.4176e-12, 1.1625e+33],\n",
" [8.9605e-01, 1.1632e+33, 5.6003e-02]])"
"tensor([[ 1.2516e-36, 0.0000e+00, 2.3822e-44],\n",
" [ 0.0000e+00, nan, 4.5743e-41],\n",
" [ 1.3733e-14, 1.8888e+31, 4.9656e+28],\n",
" [ 4.5439e+30, -4.2010e+25, 4.5743e-41],\n",
" [-4.2210e+25, 4.5743e-41, -4.2210e+25]])"
]
},
"execution_count": 2,
@@ -67,11 +67,11 @@
{
"data": {
"text/plain": [
"tensor([[0.4157, 0.7456, 0.9620],\n",
" [0.3965, 0.8182, 0.7723],\n",
" [0.3705, 0.9292, 0.0063],\n",
" [0.4054, 0.9137, 0.9611],\n",
" [0.8307, 0.0900, 0.6887]])"
"tensor([[0.1878, 0.1306, 0.1593],\n",
" [0.2964, 0.3927, 0.7782],\n",
" [0.8448, 0.4487, 0.7916],\n",
" [0.0550, 0.7300, 0.2901],\n",
" [0.8453, 0.8734, 0.2627]])"
]
},
"execution_count": 3,
@@ -122,20 +122,20 @@
},
{
"cell_type": "code",
"execution_count": 5,
"execution_count": 7,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"tensor([[0.5021, 1.2500, 1.4749],\n",
" [0.6019, 0.9378, 1.7240],\n",
" [1.2752, 1.3837, 0.6832],\n",
" [1.2053, 1.4374, 1.5160],\n",
" [0.9404, 0.8743, 0.8164]])"
"tensor([[0.9549, 1.0717, 0.4005],\n",
" [0.8394, 0.7862, 0.8726],\n",
" [1.4099, 1.3137, 1.1250],\n",
" [0.4830, 0.8297, 0.5617],\n",
" [0.9343, 0.9557, 0.9178]])"
]
},
"execution_count": 5,
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
@@ -173,20 +173,20 @@
},
{
"cell_type": "code",
"execution_count": 6,
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"tensor([[1.7112, 1.2969, 0.3289],\n",
" [0.7841, 1.0128, 0.7596],\n",
" [1.1364, 1.1541, 0.8970],\n",
" [0.8831, 0.7063, 0.3158],\n",
" [1.5160, 1.3610, 0.8437]])"
"tensor([[0.9549, 1.0717, 0.4005],\n",
" [0.8394, 0.7862, 0.8726],\n",
" [1.4099, 1.3137, 1.1250],\n",
" [0.4830, 0.8297, 0.5617],\n",
" [0.9343, 0.9557, 0.9178]])"
]
},
"execution_count": 6,
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
@@ -200,7 +200,7 @@
},
{
"cell_type": "code",
"execution_count": 7,
"execution_count": 9,
"metadata": {},
"outputs": [
{
@@ -208,23 +208,23 @@
"output_type": "stream",
"text": [
"最初y\n",
"tensor([[0.0864, 0.5044, 0.5128],\n",
" [0.2054, 0.1196, 0.9517],\n",
" [0.9047, 0.4545, 0.6769],\n",
" [0.7999, 0.5236, 0.5549],\n",
" [0.1097, 0.7843, 0.1277]])\n",
"tensor([[0.7671, 0.9411, 0.2411],\n",
" [0.5430, 0.3935, 0.0944],\n",
" [0.5652, 0.8650, 0.3334],\n",
" [0.4280, 0.0997, 0.2716],\n",
" [0.0890, 0.0823, 0.6551]])\n",
"第一种加法，y的结果\n",
"tensor([[0.0864, 0.5044, 0.5128],\n",
" [0.2054, 0.1196, 0.9517],\n",
" [0.9047, 0.4545, 0.6769],\n",
" [0.7999, 0.5236, 0.5549],\n",
" [0.1097, 0.7843, 0.1277]])\n",
"tensor([[0.7671, 0.9411, 0.2411],\n",
" [0.5430, 0.3935, 0.0944],\n",
" [0.5652, 0.8650, 0.3334],\n",
" [0.4280, 0.0997, 0.2716],\n",
" [0.0890, 0.0823, 0.6551]])\n",
"第二种加法，y的结果\n",
"tensor([[0.5021, 1.2500, 1.4749],\n",
" [0.6019, 0.9378, 1.7240],\n",
" [1.2752, 1.3837, 0.6832],\n",
" [1.2053, 1.4374, 1.5160],\n",
" [0.9404, 0.8743, 0.8164]])\n"
"tensor([[0.9549, 1.0717, 0.4005],\n",
" [0.8394, 0.7862, 0.8726],\n",
" [1.4099, 1.3137, 1.1250],\n",
" [0.4830, 0.8297, 0.5617],\n",
" [0.9343, 0.9557, 0.9178]])\n"
]
}
],
@@ -250,16 +250,16 @@
},
{
"cell_type": "code",
"execution_count": 8,
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"tensor([0.7456, 0.8182, 0.9292, 0.9137, 0.0900])"
"tensor([0.1306, 0.3927, 0.4487, 0.7300, 0.8734])"
]
},
"execution_count": 8,
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
}
@@ -280,7 +280,7 @@
},
{
"cell_type": "code",
"execution_count": 9,
"execution_count": 11,
"metadata": {},
"outputs": [
{
@@ -289,7 +289,7 @@
"tensor([1., 1., 1., 1., 1.])"
]
},
"execution_count": 9,
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
@@ -301,7 +301,7 @@
},
{
"cell_type": "code",
"execution_count": 10,
"execution_count": 13,
"metadata": {},
"outputs": [
{
@@ -310,7 +310,7 @@
"array([1., 1., 1., 1., 1.], dtype=float32)"
]
},
"execution_count": 10,
"execution_count": 13,
"metadata": {},
"output_type": "execute_result"
}
@@ -322,7 +322,7 @@
},
{
"cell_type": "code",
"execution_count": 11,
"execution_count": 14,
"metadata": {},
"outputs": [
{
@@ -351,7 +351,7 @@
},
{
"cell_type": "code",
"execution_count": 13,
"execution_count": 15,
"metadata": {},
"outputs": [
{
@@ -359,14 +359,7 @@
"output_type": "stream",
"text": [
"[2. 2. 2. 2. 2.]\n",
"\n",
" 2\n",
" 2\n",
" 2\n",
" 2\n",
" 2\n",
"[torch.DoubleTensor of size 5]\n",
"\n"
"tensor([2., 2., 2., 2., 2.], dtype=torch.float64)\n"
]
}
],
@@ -385,18 +378,18 @@
},
{
"cell_type": "code",
"execution_count": 12,
"execution_count": 16,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"tensor([[0.9177, 1.9956, 2.4369],\n",
" [0.9984, 1.7561, 2.4963],\n",
" [1.6457, 2.3129, 0.6895],\n",
" [1.6107, 2.3511, 2.4770],\n",
" [1.7711, 0.9643, 1.5050]], device='cuda:0')\n"
"tensor([[1.1427, 1.2022, 0.5598],\n",
" [1.1357, 1.1790, 1.6507],\n",
" [2.2547, 1.7623, 1.9165],\n",
" [0.5381, 1.5597, 0.8518],\n",
" [1.7796, 1.8291, 1.1805]], device='cuda:0')\n"
]
}
],
@@ -438,7 +431,7 @@
},
{
"cell_type": "code",
"execution_count": 13,
"execution_count": 17,
"metadata": {},
"outputs": [],
"source": [
@@ -447,7 +440,7 @@
},
{
"cell_type": "code",
"execution_count": 14,
"execution_count": 18,
"metadata": {
"scrolled": true
},
@@ -459,7 +452,7 @@
" [1., 1.]], requires_grad=True)"
]
},
"execution_count": 14,
"execution_count": 18,
"metadata": {},
"output_type": "execute_result"
}
@@ -472,7 +465,7 @@
},
{
"cell_type": "code",
"execution_count": 15,
"execution_count": 19,
"metadata": {
"scrolled": true
},
@@ -483,7 +476,7 @@
"tensor(4., grad_fn=<SumBackward0>)"
]
},
"execution_count": 15,
"execution_count": 19,
"metadata": {},
"output_type": "execute_result"
}
@@ -495,16 +488,16 @@
},
{
"cell_type": "code",
"execution_count": 16,
"execution_count": 20,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<SumBackward0 at 0x7f85680bd710>"
"<SumBackward0 at 0x7f8381c656d8>"
]
},
"execution_count": 16,
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
}
@@ -515,7 +508,7 @@
},
{
"cell_type": "code",
"execution_count": 17,
"execution_count": 21,
"metadata": {},
"outputs": [],
"source": [
@@ -524,7 +517,7 @@
},
{
"cell_type": "code",
"execution_count": 18,
"execution_count": 22,
"metadata": {},
"outputs": [
{
@@ -534,7 +527,7 @@
" [1., 1.]])"
]
},
"execution_count": 18,
"execution_count": 22,
"metadata": {},
"output_type": "execute_result"
}
@@ -554,7 +547,7 @@
},
{
"cell_type": "code",
"execution_count": 19,
"execution_count": 23,
"metadata": {},
"outputs": [
{
@@ -564,7 +557,7 @@
" [2., 2.]])"
]
},
"execution_count": 19,
"execution_count": 23,
"metadata": {},
"output_type": "execute_result"
}
@@ -576,7 +569,7 @@
},
{
"cell_type": "code",
"execution_count": 20,
"execution_count": 24,
"metadata": {
"scrolled": true
},
@@ -588,7 +581,7 @@
" [3., 3.]])"
]
},
"execution_count": 20,
"execution_count": 24,
"metadata": {},
"output_type": "execute_result"
}
@@ -600,7 +593,7 @@
},
{
"cell_type": "code",
"execution_count": 21,
"execution_count": 25,
"metadata": {},
"outputs": [
{
@@ -610,7 +603,7 @@
" [0., 0.]])"
]
},
"execution_count": 21,
"execution_count": 25,
"metadata": {},
"output_type": "execute_result"
}
@@ -622,7 +615,7 @@
},
{
"cell_type": "code",
"execution_count": 22,
"execution_count": 26,
"metadata": {},
"outputs": [
{
@@ -632,7 +625,7 @@
" [1., 1.]])"
]
},
"execution_count": 22,
"execution_count": 26,
"metadata": {},
"output_type": "execute_result"
}
@@ -651,7 +644,7 @@
},
{
"cell_type": "code",
"execution_count": 24,
"execution_count": 27,
"metadata": {},
"outputs": [
{
@@ -673,7 +666,7 @@
" [0.5403, 0.5403, 0.5403, 0.5403, 0.5403]])"
]
},
"execution_count": 24,
"execution_count": 27,
"metadata": {},
"output_type": "execute_result"
}
@@ -690,7 +683,7 @@
"cell_type": "markdown",
"metadata": {},
"source": [
"## 3. 神经网络\n",
"## 3. 神经网络 (FIXME)\n",
"\n",
"Autograd实现了反向传播功能，但是直接用来写深度学习的代码在很多情况下还是稍显复杂，torch.nn是专门为神经网络设计的模块化接口。nn构建于 Autograd之上，可用来定义和运行神经网络。nn.Module是nn中最重要的类，可把它看成是一个网络的封装，包含网络各层定义以及forward方法，调用forward(input)方法，可返回前向传播的结果。下面就以最早的卷积神经网络：LeNet为例，来看看如何用`nn.Module`实现。LeNet的网络结构如图2-7所示。\n",
"\n",


+ 3
- 0
References.md View File

@@ -4,6 +4,7 @@


## Notebook, Book, Tutorial

* [Deep Learning with PyTorch](https://pytorch.org/deep-learning-with-pytorch-thank-you)
* [Machine Learning Yearning 中文版 - 《机器学习训练秘籍》](https://github.com/deeplearning-ai/machine-learning-yearning-cn) ([在线阅读](https://deeplearning-ai.github.io/machine-learning-yearning-cn/))
* [ipython-notebooks: A collection of IPython notebooks covering various topics](https://github.com/jdwittenauer/ipython-notebooks)
@@ -11,6 +12,8 @@
* [AM207 2016](https://github.com/AM207/2016/tree/master)
* [Python机器学习](https://ljalphabeta.gitbooks.io/python-/content/)
* [scientific-python-lectures](http://nbviewer.jupyter.org/github/jrjohansson/scientific-python-lectures/tree/master/)
* [卷积神经网络中十大拍案叫绝的操作](https://www.toutiao.com/a6741309250070381070)



## Python & IPython


+ 3
- 2
demo_code/2_logistic_regression_1.py View File

@@ -38,12 +38,13 @@ def logistic_regression(x):

# define loss function
def binary_loss(y_pred, y):
logits = (y * y_pred.clamp(1e-12).log() + (1 - y) * (1 - y_pred).clamp(1e-12).log()).mean()
logits = (y * y_pred.clamp(1e-12).log() + \
(1 - y) * (1 - y_pred).clamp(1e-12).log()).mean()
return -logits

# upgrade parameters
eta = 1e-2
n_epoch = 1000
n_epoch = 3000

for i in range(n_epoch):
y_pred = logistic_regression(x_train)


+ 3
- 1
demo_code/2_logistic_regression_2.py View File

@@ -10,6 +10,8 @@ from torchvision import datasets
"""
Use pytorch nn.Module to implement logistic regression
FIXME: too complex, remove complete tips
"""


@@ -38,7 +40,7 @@ class Logstic_Regression(nn.Module):
self.logstic = nn.Linear(in_dim, n_class)

def forward(self, x):
out = self.logstic(x)
out = t.sigmoid(self.logstic(x))
return out




+ 5
- 1
requirements.txt View File

@@ -9,7 +9,11 @@
# sudo apt-get install python-pip python3-pip
# pip install pip -U
# pip config set global.index-url 'https://mirrors.aliyun.com/pypi/simple/'
# pip config set global.index-url 'https://mirrors.ustc.edu.cn/pypi/web/simple'
#
# or write following to '~/.config/pip/pip.conf'
# [global]
# timeout = 6000
# index-url = https://mirrors.aliyun.com/pypi/simple/
#

#


Write Preview
Loading…
Cancel
Save